Calculate Tangent Plane to Surface
This example shows how to approximate gradients of a function by finite differences. It then shows how to plot a tangent plane to a point on the surface by using these approximated gradients.
Create the function using a function handle.
f = @(x,y) x.^2 + y.^2;
Approximate the partial derivatives of with respect to and by using the gradient function. Choose a finite difference length that is the same as the mesh size.
[xx,yy] = meshgrid(-5:0.25:5); [fx,fy] = gradient(f(xx,yy),0.25);
The tangent plane to a point on the surface, , is given by
The fx and fy matrices are approximations to the partial derivatives and . The point of interest in this example, where the tangent plane meets the functional surface, is (x0,y0) = (1,2). The function value at this point of interest is f(1,2) = 5.
To approximate the tangent plane z you need to find the value of the derivatives at the point of interest. Obtain the index of that point, and find the approximate derivatives there.
x0 = 1; y0 = 2; t = (xx == x0) & (yy == y0); indt = find(t); fx0 = fx(indt); fy0 = fy(indt);
Create a function handle with the equation of the tangent plane z.
z = @(x,y) f(x0,y0) + fx0*(x-x0) + fy0*(y-y0);
Plot the original function , the point P, and a piece of plane z that is tangent to the function at P.
surf(xx,yy,f(xx,yy),'EdgeAlpha',0.7,'FaceAlpha',0.9) hold on surf(xx,yy,z(xx,yy)) plot3(1,2,f(1,2),'r*')
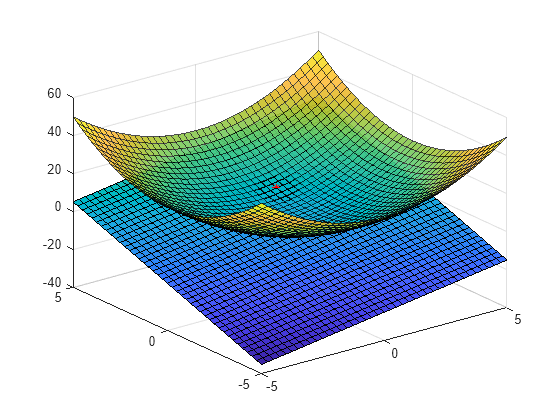
View a side profile.
view(-135,9)