Solve Nonstiff ODEs
This page contains two examples of solving nonstiff ordinary differential equations using ode45. MATLAB® has several solvers for nonstiff ODEs.
ode45ode23ode78ode89ode113
For most nonstiff problems, ode45 performs best. However, ode23 is recommended for problems that permit a slightly cruder error tolerance or in the presence of moderate stiffness. Likewise, ode113 can be more efficient than ode45 for problems with more stringent error tolerances or when the ODE function is computationally expensive to evaluate. ode78 and ode89 are high-order solvers that excel with long integrations where accuracy is crucial for stability.
If the nonstiff solvers take a long time to solve the problem or consistently fail the integration, then the problem might be stiff. See Solve Stiff ODEs for more information.
Example: Nonstiff van der Pol Equation
The van der Pol equation is a second order ODE

where  is a scalar parameter. Rewrite this equation as a system of first-order ODEs by making the substitution
is a scalar parameter. Rewrite this equation as a system of first-order ODEs by making the substitution  . The resulting system of first-order ODEs is
. The resulting system of first-order ODEs is

The system of ODEs must be coded into a function file that the ODE solver can use. The general functional signature of an ODE function is
dydt = odefun(t,y)
That is, the function must accept both t and y as inputs, even if it does not use t for any computations.
The function file vdp1.m codes the van der Pol equation using  . The variables
. The variables  and
and  are represented by
are represented by y(1) and y(2), and the two-element column vector dydt contains the expressions for  and
and  .
.
function dydt = vdp1(t,y) %VDP1 Evaluate the van der Pol ODEs for mu = 1 % % See also ODE113, ODE23, ODE45. % Jacek Kierzenka and Lawrence F. Shampine % Copyright 1984-2014 The MathWorks, Inc. dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];
Solve the ODE using the ode45 function on the time interval [0 20] with initial values [2 0]. The output is a column vector of time points t and a solution array y. Each row in y corresponds to a time returned in the corresponding row of t. The first column of y corresponds to  , and the second column to
, and the second column to  .
.
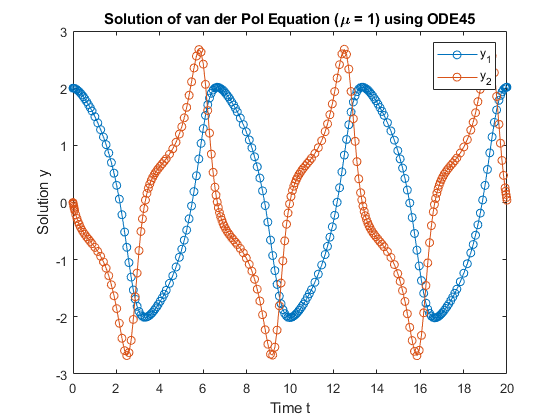
[t,y] = ode45(@vdp1,[0 20],[2; 0]);
Plot the solutions for  and
and  against
against t.
plot(t,y(:,1),'-o',t,y(:,2),'-o') title('Solution of van der Pol Equation (\mu = 1) using ODE45'); xlabel('Time t'); ylabel('Solution y'); legend('y_1','y_2')
The vdpode function solves the same problem, but it accepts a user-specified value for  . The van der Pol equations become stiff as
. The van der Pol equations become stiff as  increases. For example, with the value
increases. For example, with the value  you need to use a stiff solver such as
you need to use a stiff solver such as ode15s to solve the system.
Example: Nonstiff Euler Equations
The Euler equations for a rigid body without external forces are a standard test problem for ODE solvers intended for nonstiff problems.
The equations are

The function file rigidode defines and solves this first-order system of equations over the time interval [0 12], using the vector of initial conditions [0; 1; 1] corresponding to the initial values of  ,
,  , and
, and  . The local function
. The local function f(t,y) encodes the system of equations.
rigidode calls ode45 with no output arguments, so the solver uses the default output function odeplot to automatically plot the solution points after each step.
function rigidode %RIGIDODE Euler equations of a rigid body without external forces. % A standard test problem for non-stiff solvers proposed by Krogh. The % analytical solutions are Jacobian elliptic functions, accessible in % MATLAB. The interval here is about 1.5 periods; it is that for which % solutions are plotted on p. 243 of Shampine and Gordon. % % L. F. Shampine and M. K. Gordon, Computer Solution of Ordinary % Differential Equations, W.H. Freeman & Co., 1975. % % See also ODE45, ODE23, ODE113, FUNCTION_HANDLE. % Mark W. Reichelt and Lawrence F. Shampine, 3-23-94, 4-19-94 % Copyright 1984-2014 The MathWorks, Inc. tspan = [0 12]; y0 = [0; 1; 1]; % solve the problem using ODE45 figure; ode45(@f,tspan,y0); % -------------------------------------------------------------------------- function dydt = f(t,y) dydt = [ y(2)*y(3) -y(1)*y(3) -0.51*y(1)*y(2) ];
Solve the nonstiff Euler equations by calling the rigidode function.
rigidode title('Solution of Rigid Body w/o External Forces using ODE45') legend('y_1','y_2','y_3','Location','Best')

See Also
ode45 | ode23 | ode78 | ode89 | ode113