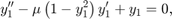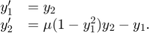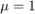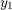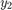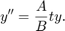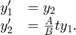ode23
Solve nonstiff differential equations — low order method
Syntax
Description
[,
where t,y] =
ode23(odefun,tspan,y0)tspan = [t0 tf], integrates the system of
differential equations from t0 to tf with
initial conditions y0. Each row in the solution
array y corresponds to a value returned in column
vector t.
All MATLAB® ODE solvers can solve systems of equations of
the form ,
or problems that involve a mass matrix, .
The solvers all use similar syntaxes. The ode23s solver
only can solve problems with a mass matrix if the mass matrix is constant. ode15s and ode23t can
solve problems with a mass matrix that is singular, known as differential-algebraic
equations (DAEs). Specify the mass matrix using the Mass option
of odeset.
[ additionally
finds where functions of (t,y),
called event functions, are zero. In the output, t,y,te,ye,ie]
= ode23(odefun,tspan,y0,options)te is
the time of the event, ye is the solution at the
time of the event, and ie is the index of the triggered
event.
For each event function, specify whether the integration is
to terminate at a zero and whether the direction of the zero crossing
matters. Do this by setting the 'Events' property
to a function, such as myEventFcn or @myEventFcn,
and creating a corresponding function: [value,isterminal,direction]
= myEventFcn(t,y).
For more information, see ODE Event Location.
sol = ode23(___)deval to evaluate
the solution at any point on the interval [t0 tf].
You can use any of the input argument combinations in previous syntaxes.
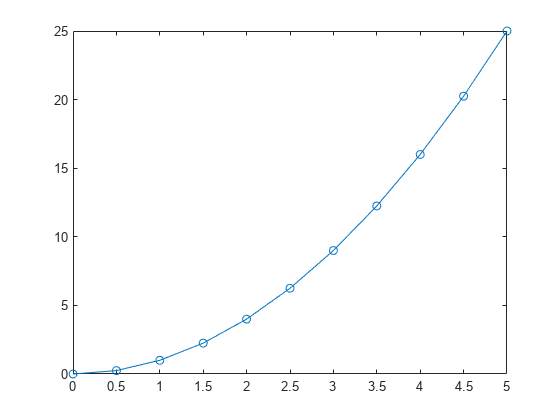
Examples
Input Arguments
Output Arguments
Algorithms
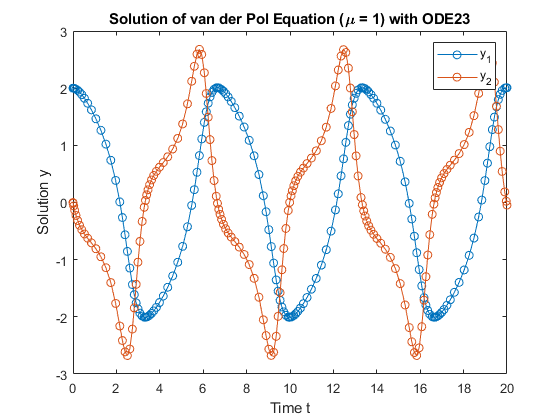
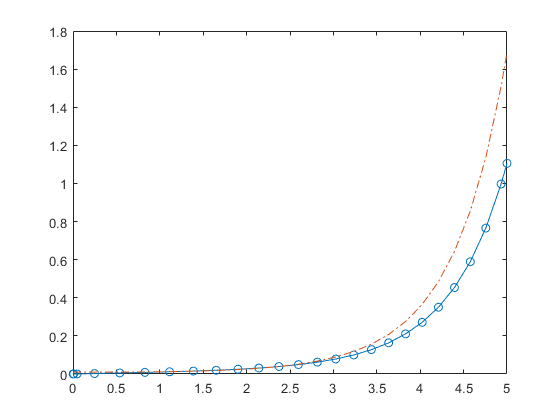
ode23 is an implementation of an explicit
Runge-Kutta (2,3) pair of Bogacki and Shampine. It may be more efficient
than ode45 at crude tolerances and in the presence
of moderate stiffness. ode23 is a single-step
solver [1], [2].
References
[1] Bogacki, P. and L. F. Shampine, “A 3(2) pair of Runge-Kutta formulas,” Appl. Math. Letters, Vol. 2, 1989, pp. 321–325.
[2] Shampine, L. F. and M. W. Reichelt, “The MATLAB ODE Suite,” SIAM Journal on Scientific Computing, Vol. 18, 1997, pp. 1–22.
Extended Capabilities
Version History
Introduced before R2006a