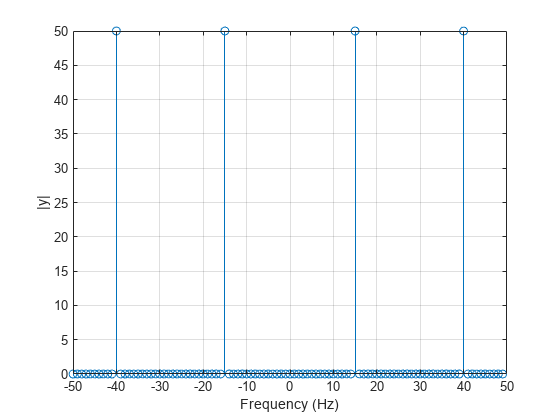
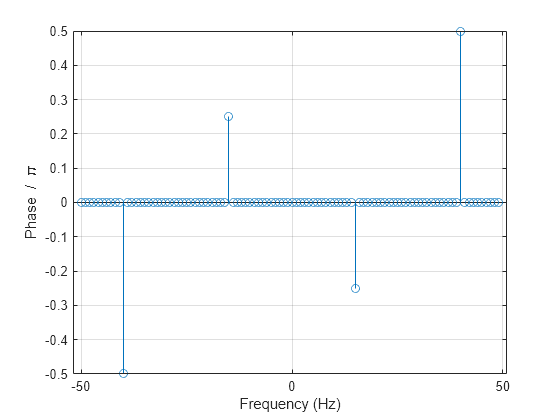
angle

Phase angle

Syntax

theta = angle(z)

Description

theta = angle(z) returns the phase angle in the interval [-π,π] for each element of a complex array z. The angles in theta are such that z = abs(z).*exp(i*theta).

Examples

Magnitude and Phase of Complex Number

Create a complex number, and compute its magnitude and phase.

z = 2*exp(i*0.5)

z = 1.7552 + 0.9589i

r = abs(z)

r = 2

theta = angle(z)

theta = 0.5000

FFT Phase

Create a signal that consists of two sinusoids of frequencies 15 Hz and 40 Hz. The first sinusoid has a phase of $-\pi /4$, and the second has a phase of $\pi /2$. Sample the signal at 100 Hz for one second.

fs = 100;
t = 0:1/fs:1-1/fs;
x = cos(2*pi*15*t - pi/4) - sin(2*pi*40*t);

Compute the Fourier transform of the signal. Plot the magnitude of the transform as a function of frequency.

y = fft(x);
z = fftshift(y);

ly = length(y);
f = (-ly/2:ly/2-1)/ly*fs;

stem(f,abs(z))
xlabel 'Frequency (Hz)'
ylabel '|y|'
grid

Compute the phase of the transform, removing small-magnitude transform values. Plot the phase as a function of frequency.

tol = 1e-6;
z(abs(z) < tol) = 0;

theta = angle(z);

stem(f,theta/pi)
xlabel 'Frequency (Hz)'
ylabel 'Phase / \pi'
grid

Input Arguments

z — Input array

scalar | vector | matrix | multidimensional array

Input array, specified as a scalar, vector, matrix, or multidimensional array. When the elements of z are non-negative real numbers, angle returns 0. When the elements of z are negative real numbers, angle returns π.

Data Types: double | single
Complex Number Support: Yes

Algorithms

angle takes a complex number z = x + iy and uses the atan2 function to compute the angle between the positive x-axis and a ray from the origin to the point (x,y) in the xy-plane.

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

This function fully supports tall arrays. For more information, see Tall Arrays.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays

Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a