fill
Create filled 2-D patches
Description
fill(
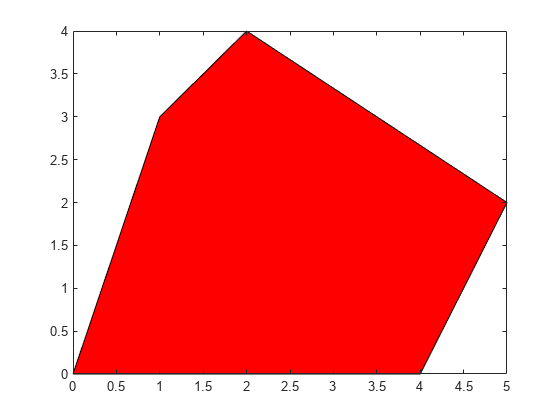
plots filled polygonal regions as patches with vertices at the
(x,y) locations specified by X,Y,C)X
and Y.
To plot one region, specify
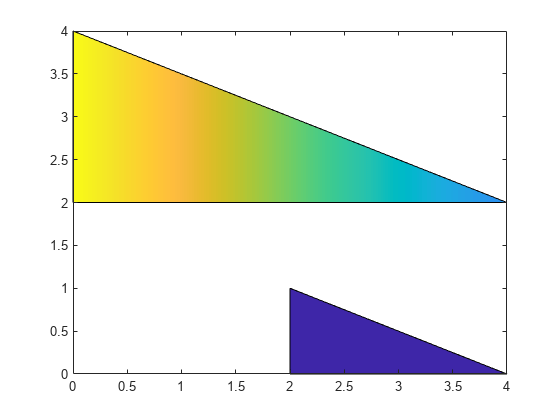
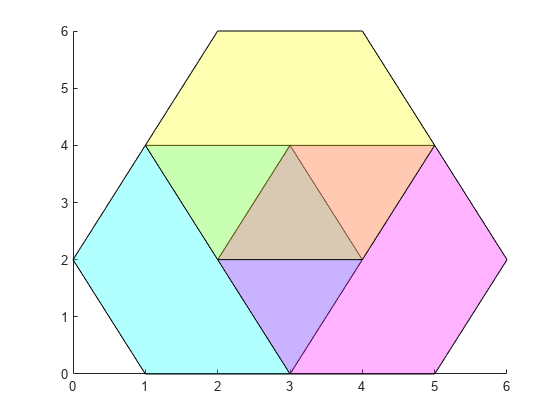
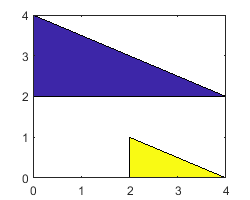
XandYas vectors.To plot multiple regions, specify
XandYas matrices where each column corresponds to a polygon.
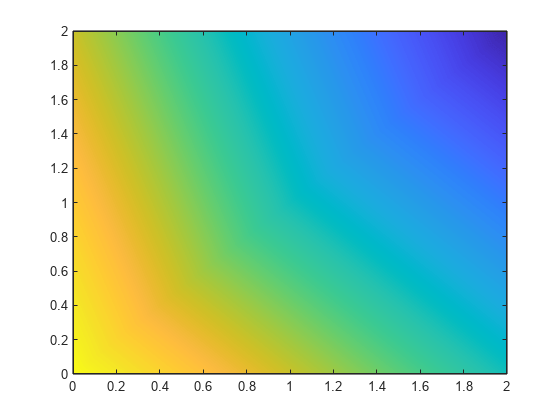
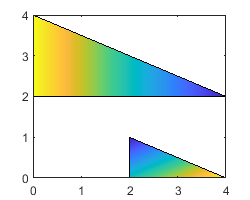
C determines the fill colors for the regions.
fill(___, modifies the
patches using one or more name-value arguments to set properties. Patches can be specified
using any of the input argument combinations in previous syntaxes. For example,
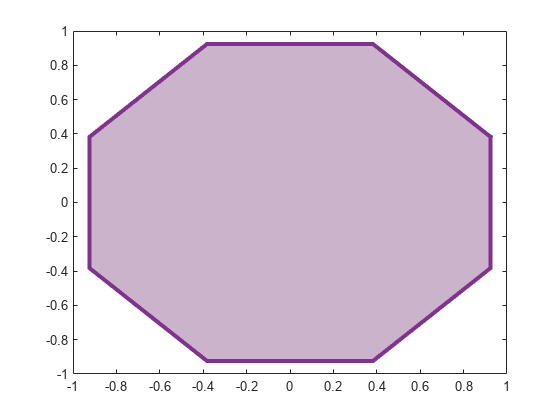
Name,Value)fill(X,Y,C,'LineWidth',2) specifies a two-point border around all the
patches. For a list of properties, see Patch Properties.
fill( plots the polygonal
regions in the axes specified by ax,___)ax instead of in the current axes (gca).
The argument ax can precede any of the input argument combinations in the
previous syntaxes.
p = fill(___)Patch object or a vector of Patch objects. Use
p to query and modify properties after plotting a region. For a list of
properties, see Patch Properties.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Alternative Functionality
Several functions offer all of the functionality of fill as well as
additional options for plotting, manipulating, and querying polygons. Use these functions in
place of fill when appropriate:
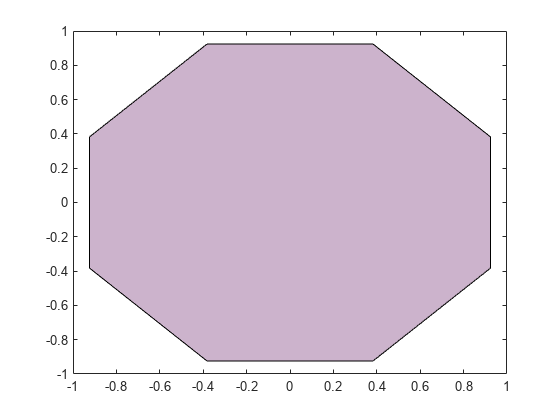
To create regular polygons, use
nsidedpoly. This function simplifies creation of regular polygons and offers additional options for managing the position and dimensions of a plotted polygon.nsidedpolycreates apolyshapeobject, with additional options for altering the location, radius, and side length of thepolyshapeafter its creation. Apolyshapecreated withnsidedpolycan be manipulated using all properties ofpolyshapeas well as the properties exclusive tonsidedpoly.To create irregular polygons, use
polyshape. This function offers additional options for defining polygons.polyshapecreates apolyshapeobject, which has additional properties and object functions for querying and altering a polygon after its creation. For a complete list, seepolyshape.To create
Patchobjects asfilldoes, usepatch. This function offers additional options for defining both 2-D and 3-D patches by their face and vertex data.