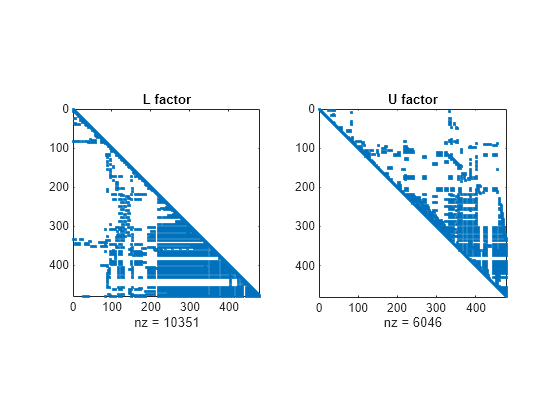
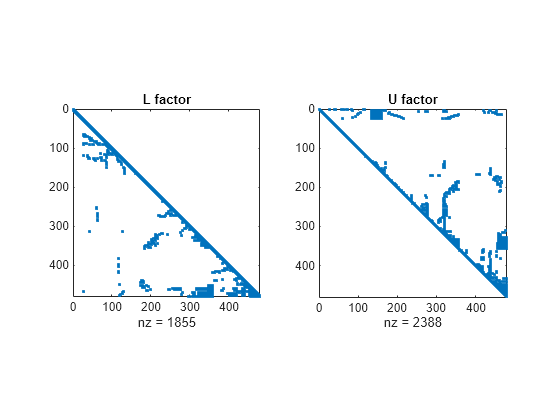
lu
LU matrix factorization
Syntax
Description
[___] = lu(
specifies thresholds for the pivoting strategy employed by
S,thresh)lu using any of the previous output argument
combinations. Depending on the number of output arguments specified, the default
value and requirements for the thresh input are different.
See the thresh argument description for details.
[___] = lu(___,
returns outputForm)P and Q in the form specified by
outputForm. Specify outputForm as
'vector' to return P and
Q as permutation vectors. You can use any of the input
argument combinations in previous syntaxes.
Examples
Input Arguments
Output Arguments
Algorithms
The LU factorization is computed using a variant of Gaussian elimination. Computing an
accurate solution is dependent upon the value of the condition number of the original
matrix cond(A). If the matrix has a large condition number (it is
nearly singular), then the computed factorization might not be accurate.
The LU factorization is a key step in obtaining the inverse with
inv and the determinant with det. It is also
the basis for the linear equation solution or matrix division obtained with the
operators \ and /. This necessarily means that the
numerical limitations of lu are also present in these dependent
functions.
References
[1] Gilbert, John R., and Tim Peierls. “Sparse Partial Pivoting in Time Proportional to Arithmetic Operations.” SIAM Journal on Scientific and Statistical Computing 9, no. 5 (September 1988): 862–874. https://doi.org/10.1137/0909058.
[2] Anderson, E., ed. LAPACK Users’ Guide. 3rd ed. Software, Environments, Tools. Philadelphia: Society for Industrial and Applied Mathematics, 1999. https://doi.org/10.1137/1.9780898719604.
[3] Davis, Timothy A. "Algorithm 832: UMFPACK V4.3 – an unsymmetric-pattern multifrontal method." ACM Transactions on Mathematical Software 30, no. 2 (June 2004): 196–199. https://doi.org/10.1145/992200.992206.