Inertial Sensor Noise Analysis Using Allan Variance
This example shows how to use the Allan variance to determine noise parameters of a MEMS gyroscope. These parameters can be used to model the gyroscope in simulation. The gyroscope measurement is modeled as:
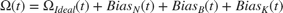
The three noise parameters N (angle random walk), K (rate random walk), and B (bias instability) are estimated using data logged from a stationary gyroscope.
Background
Allan variance was originally developed by David W. Allan to measure the frequency stability of precision oscillators. It can also be used to identify various noise sources present in stationary gyroscope measurements. Consider L samples of data from a gyroscope with a sample time of 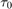 . Form data clusters of durations
. Form data clusters of durations 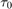 ,
, 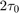 , ...,
, ..., 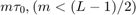 and obtain the averages of the sum of the data points contained in each cluster over the length of the cluster. The Allan variance is defined as the two-sample variance of the data cluster averages as a function of cluster time. This example uses the overlapping Allan variance estimator. This means that the calculated clusters are overlapping. The estimator performs better than non-overlapping estimators for larger values of L.
and obtain the averages of the sum of the data points contained in each cluster over the length of the cluster. The Allan variance is defined as the two-sample variance of the data cluster averages as a function of cluster time. This example uses the overlapping Allan variance estimator. This means that the calculated clusters are overlapping. The estimator performs better than non-overlapping estimators for larger values of L.
Allan Variance Calculation
The Allan variance is calculated as follows:
Log L stationary gyroscope samples with a sample period 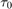 . Let
. Let  be the logged samples.
be the logged samples.
% Load logged data from one axis of a three-axis gyroscope. This recording % was done over a six hour period, with a 100 Hz sampling rate. The unit of % the gyroscope data is in radians per second. load('LoggedSingleAxisGyroscope', 'omega', 'Fs') t0 = 1/Fs;
For each sample, calculate the output angle 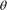 :
:
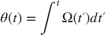
For discrete samples, the cumulative sum multiplied by 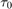 can be used.
can be used.
theta = cumsum(omega, 1)*t0;
Next, calculate the Allan variance:
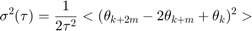
where 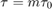 and
and 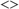 is the ensemble average.
is the ensemble average.
The ensemble average can be expanded to:
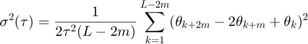
maxNumM = 100; L = size(theta, 1); maxM = 2.^floor(log2(L/2)); m = logspace(log10(1), log10(maxM), maxNumM).'; m = ceil(m); % m must be an integer. m = unique(m); % Remove duplicates. tau = m*t0; avar = zeros(numel(m), 1); for i = 1:numel(m) mi = m(i); avar(i,:) = sum( ... (theta(1+2*mi:L) - 2*theta(1+mi:L-mi) + theta(1:L-2*mi)).^2, 1); end avar = avar ./ (2*tau.^2 .* (L - 2*m));
Finally, the Allan deviation 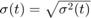 is used to determine the gyroscope noise parameters.
is used to determine the gyroscope noise parameters.
adev = sqrt(avar); figure loglog(tau, adev) title('Allan Deviation') xlabel('\tau'); ylabel('\sigma(\tau)') grid on axis equal
The Allan variance can also be calculated using the allanvar function.
[avarFromFunc, tauFromFunc] = allanvar(omega, m, Fs); adevFromFunc = sqrt(avarFromFunc); figure loglog(tau, adev, tauFromFunc, adevFromFunc); title('Allan Deviations') xlabel('\tau') ylabel('\sigma(\tau)') legend('Manual Calculation', 'allanvar Function') grid on axis equal
Noise Parameter Identification
To obtain the noise parameters for the gyroscope, use the following relationship between the Allan variance and the two-sided power spectral density (PSD) of the noise parameters in the original data set  . The relationship is:
. The relationship is:
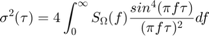
From the above equation, the Allan variance is proportional to the total noise power of the gyroscope when passed through a filter with a transfer function of 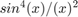 . This transfer function arises from the operations done to create and operate on the clusters.
. This transfer function arises from the operations done to create and operate on the clusters.
Using this transfer function interpretation, the filter bandpass depends on  . This means that different noise parameters can be identified by changing the filter bandpass, or varying
. This means that different noise parameters can be identified by changing the filter bandpass, or varying  .
.
Angle Random Walk
The angle random walk is characterized by the white noise spectrum of the gyroscope output. The PSD is represented by:
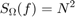
where
N = angle random walk coefficient
Substituting into the original PSD equation and performing integration yields:
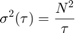
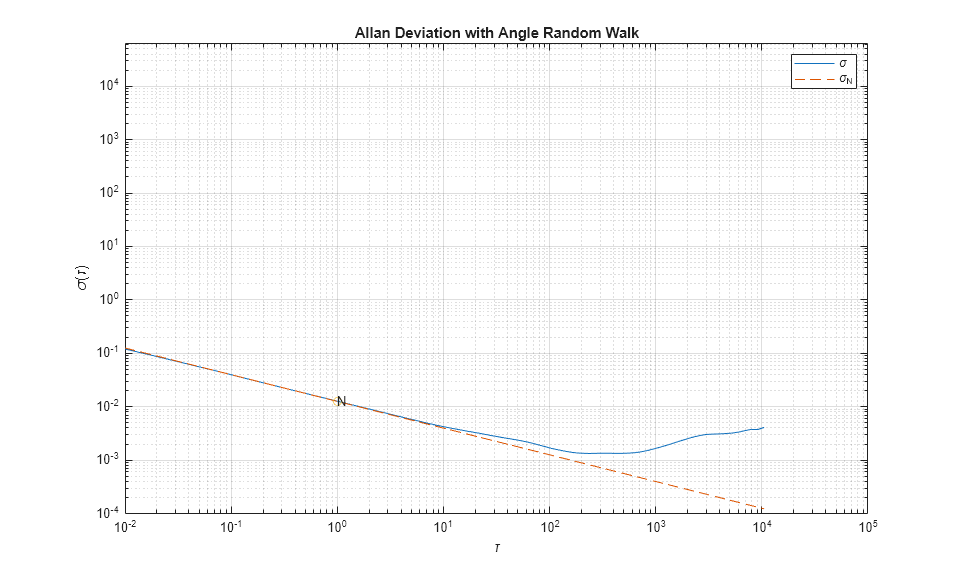
The above equation is a line with a slope of -1/2 when plotted on a log-log plot of 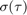 versus
versus  . The value of N can be read directly off of this line at
. The value of N can be read directly off of this line at 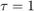 . The units of N are
. The units of N are 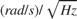 .
.
% Find the index where the slope of the log-scaled Allan deviation is equal % to the slope specified. slope = -0.5; logtau = log10(tau); logadev = log10(adev); dlogadev = diff(logadev) ./ diff(logtau); [~, i] = min(abs(dlogadev - slope)); % Find the y-intercept of the line. b = logadev(i) - slope*logtau(i); % Determine the angle random walk coefficient from the line. logN = slope*log(1) + b; N = 10^logN % Plot the results. tauN = 1; lineN = N ./ sqrt(tau); figure loglog(tau, adev, tau, lineN, '--', tauN, N, 'o') title('Allan Deviation with Angle Random Walk') xlabel('\tau') ylabel('\sigma(\tau)') legend('\sigma', '\sigma_N') text(tauN, N, 'N') grid on axis equal
N =
0.0126
Rate Random Walk
The rate random walk is characterized by the red noise (Brownian noise) spectrum of the gyroscope output. The PSD is represented by:
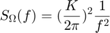
where
K = rate random walk coefficient
Substituting into the original PSD equation and performing integration yields:
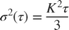
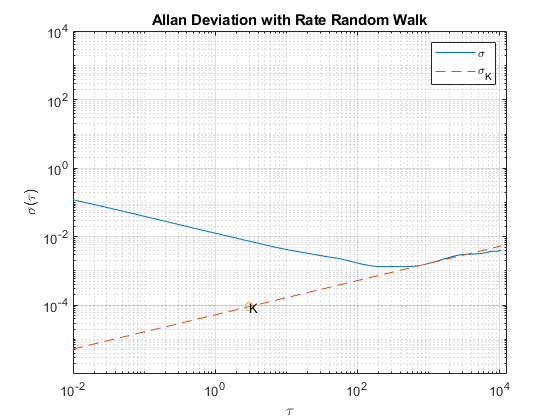
The above equation is a line with a slope of 1/2 when plotted on a log-log plot of 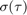 versus
versus  . The value of K can be read directly off of this line at
. The value of K can be read directly off of this line at 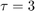 . The units of K are
. The units of K are 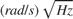 .
.
% Find the index where the slope of the log-scaled Allan deviation is equal % to the slope specified. slope = 0.5; logtau = log10(tau); logadev = log10(adev); dlogadev = diff(logadev) ./ diff(logtau); [~, i] = min(abs(dlogadev - slope)); % Find the y-intercept of the line. b = logadev(i) - slope*logtau(i); % Determine the rate random walk coefficient from the line. logK = slope*log10(3) + b; K = 10^logK % Plot the results. tauK = 3; lineK = K .* sqrt(tau/3); figure loglog(tau, adev, tau, lineK, '--', tauK, K, 'o') title('Allan Deviation with Rate Random Walk') xlabel('\tau') ylabel('\sigma(\tau)') legend('\sigma', '\sigma_K') text(tauK, K, 'K') grid on axis equal
K = 9.0679e-05
Bias Instability
The bias instability is characterized by the pink noise (flicker noise) spectrum of the gyroscope output. The PSD is represented by:
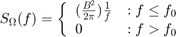
where
B = bias instability coefficient
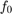 = cut-off frequency
= cut-off frequency
Substituting into the original PSD equation and performing integration yields:
![$$\sigma^2(\tau) = \frac{2B^2}{\pi}[\ln{2} + \\ -\frac{sin^3x}{2x^2}(sinx + 4xcosx) + Ci(2x) - Ci(4x)]$$](../../examples/shared_positioning/win64/AllanVarianceExample_eq05741459843801261458.png)
where
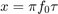
Ci = cosine-integral function
When  is much longer than the inverse of the cutoff frequency, the PSD equation is:
is much longer than the inverse of the cutoff frequency, the PSD equation is:
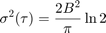
The above equation is a line with a slope of 0 when plotted on a log-log plot of 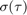 versus
versus  . The value of B can be read directly off of this line with a scaling of
. The value of B can be read directly off of this line with a scaling of 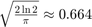 . The units of B are
. The units of B are 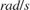 .
.
% Find the index where the slope of the log-scaled Allan deviation is equal % to the slope specified. slope = 0; logtau = log10(tau); logadev = log10(adev); dlogadev = diff(logadev) ./ diff(logtau); [~, i] = min(abs(dlogadev - slope)); % Find the y-intercept of the line. b = logadev(i) - slope*logtau(i); % Determine the bias instability coefficient from the line. scfB = sqrt(2*log(2)/pi); logB = b - log10(scfB); B = 10^logB % Plot the results. tauB = tau(i); lineB = B * scfB * ones(size(tau)); figure loglog(tau, adev, tau, lineB, '--', tauB, scfB*B, 'o') title('Allan Deviation with Bias Instability') xlabel('\tau') ylabel('\sigma(\tau)') legend('\sigma', '\sigma_B') text(tauB, scfB*B, '0.664B') grid on axis equal
B =
0.0020
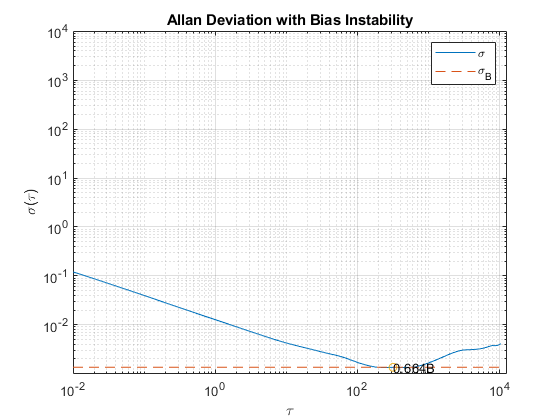
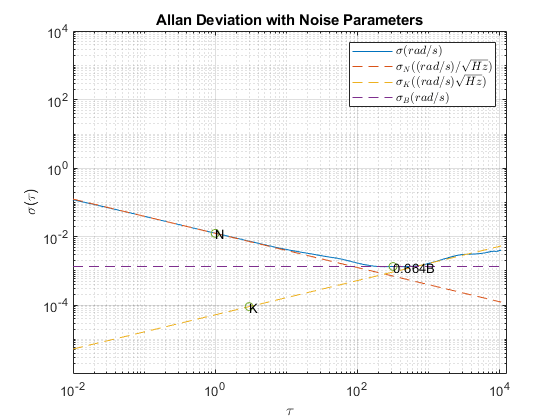
Now that all the noise parameters have been calculated, plot the Allan deviation with all of the lines used for quantifying the parameters.
tauParams = [tauN, tauK, tauB]; params = [N, K, scfB*B]; figure loglog(tau, adev, tau, [lineN, lineK, lineB], '--', ... tauParams, params, 'o') title('Allan Deviation with Noise Parameters') xlabel('\tau') ylabel('\sigma(\tau)') legend('$\sigma (rad/s)$', '$\sigma_N ((rad/s)/\sqrt{Hz})$', ... '$\sigma_K ((rad/s)\sqrt{Hz})$', '$\sigma_B (rad/s)$', 'Interpreter', 'latex') text(tauParams, params, {'N', 'K', '0.664B'}) grid on axis equal
Gyroscope Simulation
Use the imuSensor object to simulate gyroscope measurements with the noise parameters identified above.
% Simulating the gyroscope measurements takes some time. To avoid this, the % measurements were generated and saved to a MAT-file. By default, this % example uses the MAT-file. To generate the measurements instead, change % this logical variable to true. generateSimulatedData = false; if generateSimulatedData % Set the gyroscope parameters to the noise parameters determined % above. Use single-sided noise to match the parameter scaling and 500 % poles for the bias instability model to match the hardware output. numpoles = 500; gyro = gyroparams('NoiseDensity', N, 'RandomWalk', K, ... 'BiasInstability', B, 'NoiseType', 'single-sided', ... 'BiasInstabilityCoefficients', fractalcoef(numpoles)); omegaSim = helperAllanVarianceExample(L, Fs, gyro); else load('SimulatedSingleAxisGyroscope', 'omegaSim') end
Calculate the simulated Allan deviation and compare it to the logged data.
[avarSim, tauSim] = allanvar(omegaSim, 'octave', Fs); adevSim = sqrt(avarSim); adevSim = mean(adevSim, 2); % Use the mean of the simulations. figure loglog(tau, adev, tauSim, adevSim, '--') title('Allan Deviation of HW and Simulation') xlabel('\tau'); ylabel('\sigma(\tau)') legend('HW', 'SIM') grid on axis equal
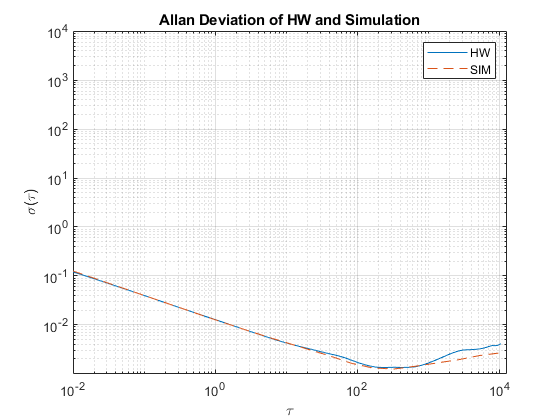
The plot shows that the gyroscope model created from the imuSensor generates measurements with similar Allan deviation to the logged data. The model measurements contain slightly less noise since the quantization and temperature-related parameters are not set using gyroparams. The gyroscope model can be used to generate measurements using movements that are not easily captured with hardware.
References
IEEE Std. 647-2006 IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros