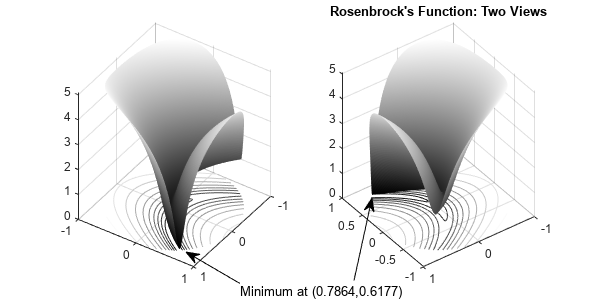
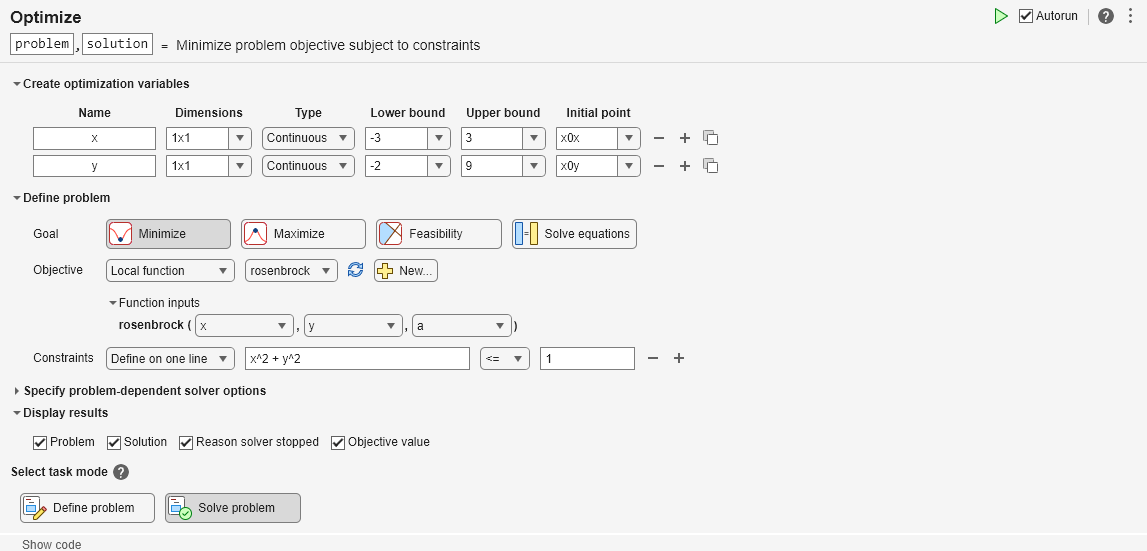
Problem-Based Optimization Setup
In problem-based optimization you create optimization variables,
expressions in these variables that represent the objective and constraints
or that represent equations, and solve the problem using solve. For the problem-based steps to take for optimization
problems, see Problem-Based Optimization Workflow. For
equation-solving, see Problem-Based Workflow for Solving Equations. To
decide between the problem-based and solver-based approaches, see First Choose Problem-Based or Solver-Based Approach.
If you have a nonlinear function that is not composed of polynomials,
rational expressions, and elementary functions such as
exp, then convert the function to an optimization
expression by using fcn2optimexpr. See Convert Nonlinear Function to Optimization Expression and
Supported Operations for Optimization Variables and Expressions.
Categories
- Get Started with Problem-Based Optimization and Equations
Get started with problem-based setup
- Improve Problem-Based Organization and Performance
Implement specialized tasks in problem-based setup