Fit ODE Parameters Using Optimization Variables
This example shows how to find parameters that optimize an ordinary differential equation (ODE) in the least-squares sense, using optimization variables (the problem-based approach).
Problem
The problem is a multistep reaction model involving several substances, some of which react with each other to produce different substances.
For this problem, the true reaction rates are unknown. So, you need to observe the reactions and infer the rates. Assume that you can measure the substances for a set of times . From these observations, fit the best set of reaction rates to the measurements.
Model
The model has six substances, through , that react as follows:
One and one react to form one at rate
One and one react to form one at rate
One and one react to form one at rate

The reaction rate is proportional to the product of the quantities of the required substances. So, if represents the quantity of substance , then the reaction rate to produce is . Similarly, the reaction rate to produce is , and the reaction rate to produce is .
In other words, the differential equation controlling the evolution of the system is
Start the differential equation at time 0 at the point . These initial values ensure that all of the substances react completely, causing through to approach zero as time increases.
Express Model in MATLAB
The diffun function implements the differential equations in a form ready for solution by ode45.
type diffunfunction dydt = diffun(~,y,r) dydt = zeros(6,1); s12 = y(1)*y(2); s34 = y(3)*y(4); dydt(1) = -r(1)*s12; dydt(2) = -r(1)*s12; dydt(3) = -r(2)*s34 + r(1)*s12 - r(3)*s34; dydt(4) = -r(2)*s34 - r(3)*s34; dydt(5) = r(2)*s34; dydt(6) = r(3)*s34; end
The true reaction rates are , , and . Compute the evolution of the system for times zero through five by calling ode45.
rtrue = [2.5 1.2 0.45]; y0 = [1 1 0 1 0 0]; tspan = linspace(0,5); soltrue = ode45(@(t,y)diffun(t,y,rtrue),tspan,y0); yvalstrue = deval(soltrue,tspan); for i = 1:6 subplot(3,2,i) plot(tspan,yvalstrue(i,:)) title(['y(',num2str(i),')']) end

Optimization Problem
To prepare the problem for solution in the problem-based approach, create a three-element optimization variable r that has a lower bound of 0.1 and an upper bound of 10.
r = optimvar('r',3,"LowerBound",0.1,"UpperBound",10);
The objective function for this problem is the sum of squares of the differences between the ODE solution with parameters r and the solution with the true parameters yvals. To express this objective function, first write a MATLAB function that computes the ODE solution using parameters r. This function is the RtoODE function.
type RtoODEfunction solpts = RtoODE(r,tspan,y0) sol = ode45(@(t,y)diffun(t,y,r),tspan,y0); solpts = deval(sol,tspan); end
To use RtoODE in an objective function, convert the function to an optimization expression by using fcn2optimexpr. See Convert Nonlinear Function to Optimization Expression.
myfcn = fcn2optimexpr(@RtoODE,r,tspan,y0);
Express the objective function as the sum of squared differences between the ODE solution and the solution with true parameters.
obj = sum(sum((myfcn - yvalstrue).^2));
Create an optimization problem with the objective function obj.
prob = optimproblem("Objective",obj);Solve Problem
To find the best-fitting parameters r, give an initial guess r0 for the solver and call solve.
r0.r = [1 1 1]; [rsol,sumsq] = solve(prob,r0)
Solving problem using lsqnonlin. Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>
rsol = struct with fields:
r: [3×1 double]
sumsq = 3.8659e-15
The sum of squared differences is essentially zero, meaning the solver found parameters that cause the ODE solution to match the solution with true parameters. So, as expected, the solution contains the true parameters.
disp(rsol.r)
2.5000
1.2000
0.4500
disp(rtrue)
2.5000 1.2000 0.4500
Limited Observations
Suppose that you cannot observe all the components of y, but only the final outputs y(5) and y(6). Can you obtain the values of all the reaction rates based on this limited information?
To find out, modify the function RtoODE to return only the fifth and sixth ODE outputs. The modified ODE solver is in RtoODE2.
type RtoODE2function solpts = RtoODE2(r,tspan,y0) solpts = RtoODE(r,tspan,y0); solpts = solpts([5,6],:); % Just y(5) and y(6) end
The RtoODE2 function simply calls RtoODE and then takes the final two rows of the output.
Create a new optimization expression from RtoODE2 and the optimization variable r, the time span data tspan, and the initial point y0.
myfcn2 = fcn2optimexpr(@RtoODE2,r,tspan,y0);
Modify the comparison data to include outputs 5 and 6 only.
yvals2 = yvalstrue([5,6],:);
Create a new objective and new optimization problem from the optimization expression myfcn2 and the comparison data yvals2.
obj2 = sum(sum((myfcn2 - yvals2).^2));
prob2 = optimproblem("Objective",obj2);Solve the problem based on this limited set of observations.
[rsol2,sumsq2] = solve(prob2,r0)
Solving problem using lsqnonlin. Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance. <stopping criteria details>
rsol2 = struct with fields:
r: [3×1 double]
sumsq2 = 2.1616e-05
Once again, the returned sum of squares is essentially zero. Does this mean that the solver found the correct reaction rates?
disp(rsol2.r)
1.7811
1.5730
0.5899
disp(rtrue)
2.5000 1.2000 0.4500
No; in this case, the new rates are quite different from the true rates. However, a plot of the new ODE solution compared to the true values shows that y(5) and y(6) match the true values.
figure plot(tspan,yvals2(1,:),'b-') hold on ss2 = RtoODE2(rsol2.r,tspan,y0); plot(tspan,ss2(1,:),'r--') plot(tspan,yvals2(2,:),'c-') plot(tspan,ss2(2,:),'m--') legend('True y(5)','New y(5)','True y(6)','New y(6)','Location','northwest') hold off

To identify the correct reaction rates for this problem, you must have data for more observations than y(5) and y(6).
Plot all the components of the solution with the new parameters, and plot the solution with the true parameters.
figure yvals2 = RtoODE(rsol2.r,tspan,y0); for i = 1:6 subplot(3,2,i) plot(tspan,yvalstrue(i,:),'b-',tspan,yvals2(i,:),'r--') legend('True','New','Location','best') title(['y(',num2str(i),')']) end
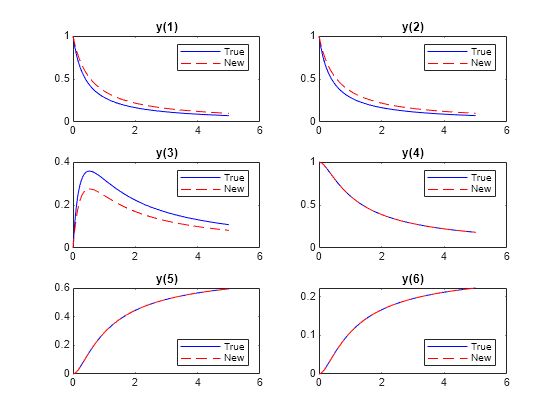
With the new parameters, substances and drain more slowly, and substance does not accumulate as much. But substances , , and have exactly the same evolution with both the new parameters and the true parameters.
See Also
solve | ode45 | fcn2optimexpr