Optimize Live Editor Task with lsqlin Solver
This example shows how to use the Optimize Live Editor task to solve a constrained least-squares problem.
The problem in this example is to find the point on the plane x1 + 2x2 + 4x3 = 7 that is closest to the origin. The easiest way to solve this problem is to minimize the square of the distance from a point x = (x1,x2,x3) on the plane to the origin, which returns the same optimal point as minimizing the actual distance. Because the square of the distance from an arbitrary point (x1,x2,x3) to the origin is , you can describe the problem as follows:
subject to the constraint
| x1 + 2x2 + 4x3 = 7. | (1) |
The function f(x) is the objective function and x1 + 2x2 + 4x3 = 7 is an equality constraint. More complicated problems might contain other equality constraints, inequality constraints, and upper or lower bound constraints.
Set Up and Solve the Problem Using Optimize
Set up the problem with the lsqlin solver in the
Optimize Live Editor task.
Create a new live script by clicking the New Live Script button in the File section on the Home tab.
Insert an Optimize Live Editor task. Click the Insert tab and then, in the Code section, select Task > Optimize.

Click the Solver-based button. The Optimize task opens.
In the Specify problem type section of the task, select Objective > Least squares and Constraints > Linear equality.
The task selects
lsqlinas the recommended solver.To get the data
Canddinto the MATLAB® workspace, click the Section Break button on the Insert tab. In the new section, enter the following code.C = eye(3); d = zeros(3,1);
Set the linear equality constraint matrix and vector.
Aeq = [1 2 4]; beq = 7;
Run the section by pressing Ctrl+Enter. This places the variables into the workspace.
In the Select problem data section of the task, set the entries to their corresponding values.

Run the solver by pressing Ctrl+Enter. View the exit message.
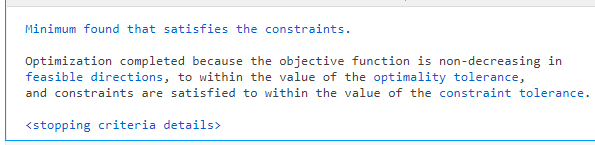
To find the solution, look at the top of the task.

The solver returns the variables
solutionandobjectiveValueto the MATLAB workspace.Insert a section break below the task. Place these lines in the new section.
disp(solution) disp(objectiveValue)
Run the section by pressing Ctrl+Enter.
![solution = [1/3, 2/3, 4/3]. objective = 7/3.](optimizelet_lsqlin_results.png)