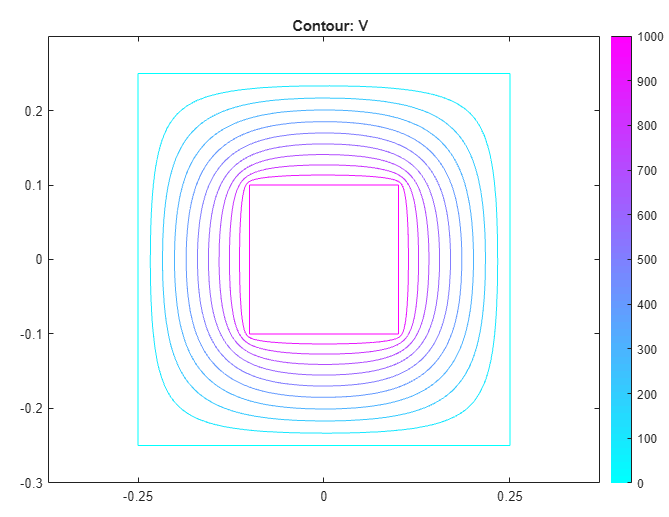
Electrostatic Potential in Air-Filled Frame: PDE Modeler App
Find the electrostatic potential in an air-filled annular quadrilateral frame using the PDE Modeler app. For this example, use the following parameters:
Inner square side is 0.2 m
Outer square side is 0.5 m
Electrostatic potential at the inner boundary is 1000V
Electrostatic potential at the outer boundary is 0V
The PDE governing this problem is the Poisson equation
–∇ · (ε∇V) = ρ.
The PDE Modeler app uses the relative permittivity εr = ε/ε0, where ε0 is the absolute dielectric permittivity of a vacuum (8.854 · 10-12 farad/meter). The relative permittivity for the air is 1.00059. Note that the coefficient of permittivity does not affect the result in this example as long as the coefficient is constant.
Assuming that there is no charge in the domain, you can simplify the Poisson equation to the Laplace equation,
ΔV = 0.
Here, the boundary conditions are the Dirichlet boundary conditions V = 1000 at the inner boundary and V = 0 at the outer boundary.
To solve this problem in the PDE Modeler app, follow these steps:
Draw the following two squares.
pderect([-0.1 0.1 -0.1 0.1]) pderect([-0.25 0.25 -0.25 0.25])
Set both x- and y-axis limits to
[-0.3 0.3]. To do this, select Options > Axes Limits and set the corresponding ranges. Then select Options > Axes Equal.Model the frame by entering
SQ2-SQ1in the Set formula field.Set the application mode to Electrostatics.
Specify the boundary conditions. To do this, switch to the boundary mode by selecting Boundary > Boundary Mode. Use Shift+click to select several boundaries. Then select Boundary > Specify Boundary Conditions.
For the inner boundaries, use the Dirichlet boundary condition with
h = 1andr = 1000.For the outer boundaries, use the Dirichlet boundary condition with
h = 1andr = 0.
Specify the coefficients by selecting PDE > PDE Specification or clicking the
 button on the toolbar.
Specify
button on the toolbar.
Specify epsilon = 1andrho = 0.Initialize the mesh by selecting Mesh > Initialize Mesh.
Solve the PDE by selecting Solve > Solve PDE or clicking the
 button on the toolbar.
button on the toolbar.Plot the equipotential lines using a contour plot. To do this, select Plot > Parameters and choose the contour plot in the resulting dialog box.
Improve the accuracy of the solution by refining the mesh close to the reentrant corners where the gradients are steep. To do this, select Solve > Parameters. Select Adaptive mode, use the Worst triangles selection method, and set the maximum number of triangles to 500. Select Mesh > Refine Mesh.
Solve the PDE using the refined mesh. To display equipotential lines at every 100th volt, select Plot > Parameters and enter
0:100:1000in the Contour plot levels field.