phased.RangeEstimator
Range estimation
Description
The phased.RangeEstimator
System object™ estimates the ranges of targets. Input to the estimator consists of a
range-response or range-Doppler response data cube, and detection locations from a
detector. When information about clusters of detections is available, the ranges are
computed using cluster information. Clustering associates multiple detections into one
extended detection.
To compute the detections for a range-response or range-Doppler cube:
Define and set up a range estimator using the Construction procedure that follows.
Call the
stepmethod to compute the range, using the properties you specify for thephased.RangeEstimatorSystem object.
Note
Instead of using the step method to perform the
operation defined by the System object, you can call the object with arguments, as if it were a function. For
example, y = step(obj,x) and y = obj(x)
perform equivalent operations.
Construction
estimator = phased.RangeEstimator creates a range estimator
System object, estimator.
estimator = phased.RangeEstimator(
creates a System object, Name,Value)estimator, with each specified property
Name set to the specified Value. You can
specify additional name and value pair arguments in any order as
(Name1,Value1,...,NameN,ValueN).
Properties
Source of the number of range estimates to report, specified as
'Auto' or 'Property'.
If you set this property to 'Auto', the number of
reported estimates is determined from the number of columns in the
detidx input to the step method. If cluster IDs are provided, the number of
estimates is determined from the number of unique cluster IDs in the
clusterids input to the step method.
If you set this property to 'Property', the number of
reported estimates is obtained from the value of the
NumEstimates property.
Data Types: char
The maximum number of range estimates to report, specified as a positive
integer. The number of requested estimates can be greater than the number of
columns in the detidx argument or the number of unique
IDs in the clusterids argument of the
step method. In that case, the remainder is filled with
NaN.
Dependencies
To enable this property, set the
NumEstimatesSource property to
'Property'.
Data Types: single | double
Option to accept cluster IDs as an input argument to the step method, specified as
false or true. Setting this
property to true enables the
clusterids input argument.
Data Types: logical
Option to enable output of range estimate variances, specified as
false or true. Range variances are
returned by the rngvar output argument of the step method.
Data Types: logical
Root-mean-square range resolution of the detection, specified as a
positive scalar. The value of the RMSResolution must
have the same units as the rangegrid input argument of
the step method.
Dependencies
To enable this property, set the value of the
VarianceOutputPort property to
true.
Data Types: single | double
Source of noise power values, specified as 'Property'
or 'Input port'. Noise power is used to compute range
estimation variance and SNR. If you set this property to
'Property', the value of the
NoisePower property represents the noise power at
the detection locations. If you set this property to 'Input
port', you can specify noise power using the
noisepower input argument, of the step method.
Data Types: char
Constant noise power value over the range-response or range-Doppler response data cube, specified as a positive real scalar. Noise power units are linear. The same noise power value is applied to all detections.
Dependencies
To enable this property, set the value of the
VarianceOutputPort property to
true and set
NoisePowerSource to
'Property'.
Data Types: single | double
Methods
| step | Estimate target range |
| Common to All System Objects | |
|---|---|
release | Allow System object property value changes |
Examples
To estimate the range and speed of three targets, create a range-Doppler map using the phased.RangeDopplerResponse System object™. Then use the phased.RangeEstimator and phased.DopplerEstimator System objects to estimate range and speed. The transmitter and receiver are collocated isotropic antenna elements forming a monostatic radar system.
The transmitted signal is a linear FM waveform with a pulse repetition interval (PRI) of 7.0 μs and a duty cycle of 2%. The operating frequency is 77 GHz and the sample rate is 150 MHz.
fs = 150e6;
c = physconst("LightSpeed");
fc = 77.0e9;
pri = 7e-6;
prf = 1/pri;Set up the scenario parameters. The transmitter and receiver are stationary and located at the origin. The targets are 500, 530, and 750 meters from the radar along the x-axis. The targets move along the x-axis at speeds of –60, 20, and 40 m/s. All three targets have a nonfluctuating radar cross-section (RCS) of 10 dB. Create the target and radar platforms.
Numtgts = 3;
tgtpos = zeros(Numtgts);
tgtpos(1,:) = [500 530 750];
tgtvel = zeros(3,Numtgts);
tgtvel(1,:) = [-60 20 40];
tgtrcs = db2pow(10)*[1 1 1];
tgtmotion = phased.Platform(tgtpos,tgtvel);
target = phased.RadarTarget(PropagationSpeed=c,OperatingFrequency=fc, ...
MeanRCS=tgtrcs);
radarpos = [0;0;0];
radarvel = [0;0;0];
radarmotion = phased.Platform(radarpos,radarvel);Create the transmitter and receiver antennas.
txantenna = phased.IsotropicAntennaElement; rxantenna = clone(txantenna);
Set up the transmitter-end signal processing. Create an upsweep linear FM signal with a bandwidth of one half the sample rate. Find the length of the PRI in samples and then estimate the rms bandwidth and range resolution.
bw = fs/2; waveform = phased.LinearFMWaveform(SampleRate=fs, ... PRF=prf,OutputFormat="Pulses",NumPulses=1,SweepBandwidth=fs/2, ... DurationSpecification="Duty cycle",DutyCycle=0.02); sig = waveform(); Nr = length(sig); bwrms = bandwidth(waveform)/sqrt(12); rngrms = c/bwrms;
Set up the transmitter and radiator System object properties. The peak output power is 10 W and the transmitter gain is 36 dB.
peakpower = 10; txgain = 36.0; transmitter = phased.Transmitter( ... PeakPower=peakpower, ... Gain=txgain, ... InUseOutputPort=true); radiator = phased.Radiator( ... Sensor=txantenna,... PropagationSpeed=c,... OperatingFrequency=fc);
Set up the free-space channel in two-way propagation mode.
channel = phased.FreeSpace( ... SampleRate=fs, ... PropagationSpeed=c, ... OperatingFrequency=fc, ... TwoWayPropagation=true);
Set up the receiver-end processing. Set the receiver gain and noise figure.
collector = phased.Collector( ... Sensor=rxantenna, ... PropagationSpeed=c, ... OperatingFrequency=fc); rxgain = 42.0; noisefig = 1; receiver = phased.ReceiverPreamp( ... SampleRate=fs, ... Gain=rxgain, ... NoiseFigure=noisefig);
Loop over the pulses to create a data cube of 128 pulses. For each step of the loop, move the target and propagate the signal. Then put the received signal into the data cube. The data cube contains the received signal per pulse. Ordinarily, a data cube has three dimensions where the last dimension corresponds to antennas or beams. Because only one sensor is used, the cube has only two dimensions.
The processing steps are:
Move the radar and targets.
Transmit a waveform.
Propagate the waveform signal to the target.
Reflect the signal from the target.
Propagate the waveform back to the radar. Two-way propagation enables you to combine the return propagation with the outbound propagation.
Receive the signal at the radar.
Load the signal into the data cube.
Np = 128; dt = pri; cube = zeros(Nr,Np); for n = 1:Np [sensorpos,sensorvel] = radarmotion(dt); [tgtpos,tgtvel] = tgtmotion(dt); [tgtrng,tgtang] = rangeangle(tgtpos,sensorpos); sig = waveform(); [txsig,txstatus] = transmitter(sig); txsig = radiator(txsig,tgtang); txsig = channel(txsig,sensorpos,tgtpos,sensorvel,tgtvel); tgtsig = target(txsig); rxcol = collector(tgtsig,tgtang); rxsig = receiver(rxcol); cube(:,n) = rxsig; end
Display the data cube containing signals per pulse.
imagesc([0:(Np-1)]*pri*1e6,[0:(Nr-1)]/fs*1e6,abs(cube)) xlabel('Slow Time {\mu}s') ylabel('Fast Time {\mu}s') axis xy
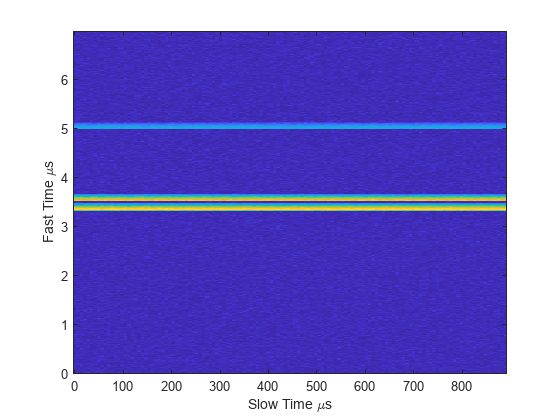
Create and display the range-Doppler image for 128 Doppler bins. The image shows range vertically and speed horizontally. Use the linear FM waveform for match filtering. The image is here is the range-Doppler map.
ndop = 128; rangedopresp = phased.RangeDopplerResponse(SampleRate=fs, ... PropagationSpeed=c,DopplerFFTLengthSource="Property", ... DopplerFFTLength=ndop,DopplerOutput="Speed", ... OperatingFrequency=fc); matchingcoeff = getMatchedFilter(waveform); [rngdopresp,rnggrid,dopgrid] = rangedopresp(cube,matchingcoeff); imagesc(dopgrid,rnggrid,10*log10(abs(rngdopresp))) xlabel("Closing Speed (m/s)") ylabel("Range (m)") axis xy
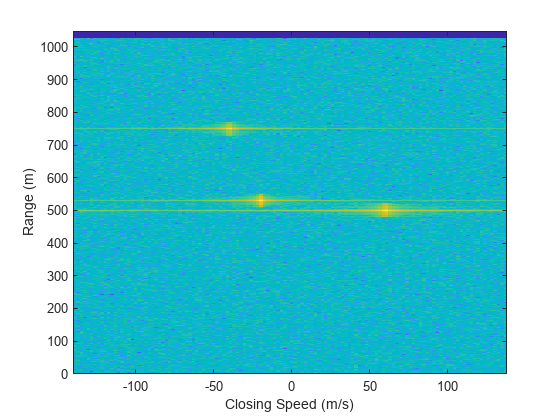
Because the targets lie along the positive x-axis, positive velocity in the global coordinate system corresponds to negative closing speed. Negative velocity in the global coordinate system corresponds to positive closing speed.
Estimate the noise power after matched filtering. Create a constant noise background image for simulation purposes.
mfgain = matchingcoeff'*matchingcoeff; dopgain = Np; noisebw = fs; noisepower = noisepow(noisebw,receiver.NoiseFigure,receiver.ReferenceTemperature); noisepowerprc = mfgain*dopgain*noisepower; noise = noisepowerprc*ones(size(rngdopresp));
Create the range and Doppler estimator objects.
rangeestimator = phased.RangeEstimator(NumEstimatesSource="Auto", ... VarianceOutputPort=true,NoisePowerSource="Input port", ... RMSResolution=rngrms); dopestimator = phased.DopplerEstimator(VarianceOutputPort=true, ... NoisePowerSource="Input port",NumPulses=Np);
Locate the target indices in the range-Doppler image. Instead of using a CFAR detector, for simplicity, use the known locations and speeds of the targets to obtain the corresponding index in the range-Doppler image.
detidx = NaN(2,Numtgts); tgtrng = rangeangle(tgtpos,radarpos); tgtspd = radialspeed(tgtpos,tgtvel,radarpos,radarvel); tgtdop = 2*speed2dop(tgtspd,c/fc); for m = 1:numel(tgtrng) [~,iMin] = min(abs(rnggrid-tgtrng(m))); detidx(1,m) = iMin; [~,iMin] = min(abs(dopgrid-tgtspd(m))); detidx(2,m) = iMin; end
Find the noise power at the detection locations.
ind = sub2ind(size(noise),detidx(1,:),detidx(2,:));
Estimate the range and range variance at the detection locations. The estimated ranges agree with the postulated ranges.
[rngest,rngvar] = rangeestimator(rngdopresp,rnggrid,detidx,noise(ind))
rngest = 3×1
499.7911
529.8380
750.0983
rngvar = 3×1
10-4 ×
0.0273
0.0276
0.2094
Estimate the speed and speed variance at the detection locations. The estimated speeds agree with the predicted speeds.
[spdest,spdvar] = dopestimator(rngdopresp,dopgrid,detidx,noise(ind))
spdest = 3×1
60.5241
-19.6167
-39.5838
spdvar = 3×1
10-5 ×
0.0806
0.0816
0.6188
More About
One input to the range estimator is a response data cube. To create a response
data cube, use the phased.RangeDopplerResponse or
phased.RangeResponse System objects.
The first dimension of the cube represents the range. Only the first dimension is
used to estimate range. All other dimensions are ignored. To interpret the detection
location, you must pass in the rnggrid vector corresponding to
the range values along this dimension. See Radar Data Cube Concept.
Algorithms
The phased.RangeEstimator
System object estimates the range of a detection by following these steps:
Input a range-processed response data cube obtained from either the
phased.RangeResponseorphased.RangeDopplerResponseSystem object. The first dimension of the cube represents the fast-time or equivalent range of the returned signal samples. Only this dimension is used to estimate detection range. All others are ignored.Input a matrix of detection indices that specify the location of detections in the data cube. Each column denotes a separate detection. The row entries designate indices into the data cube. You can obtain detection indices as an output of the
phased.CFARDetectororphased.CFARDetector2Ddetectors. To return these indices, set theOutputFormatproperty of either CFAR detector to'Detection index'.Optionally input a row vector of cluster IDs. This vector is equal in length to the number of detections. Each element of this vector assigns an ID to a corresponding detection. To form clusters of detections, the same ID can be assigned to more than one detection. To enable this option, set the
ClusterInputPortproperty totrue.When
ClusterInputPortisfalse, the object computes the range for each detection. The algorithm finds the response values at the detection location and at two adjacent indices in the cube along the range dimension. Then, the algorithm fits a quadratic curve to the magnitudes of the range response at these three locations and finds the location of the peak. When detections occur at the first or last sample in the range dimension, the range response is estimated from a two-point centroid. The estimation is at the location of the detection index and at the sample adjacent to the detection index.When
ClusterInputPortistrue, the object computes range for each cluster. The algorithm finds the indices of the largest response value in the cluster and fits a quadratic formula to that detection in the same way as for individual detections.Convert the fractional index values of the fitted peak locations to range. To convert the indices, choose appropriate units for the
rnggridinput argument of thestepmethod. You can use values forrnggridobtained from either thephased.RangeResponseorphased.RangeDopplerResponseSystem objects.
The object computes the estimated range variance using the Ziv-Zakai bound.
This System object supports single and double precision for input data, properties, and arguments. If
the input data X is single precision, the output data is single precision.
If the input data X is double precision, the output data is double
precision. The precision of the output is independent of the precision of the properties and
other arguments.
References
[1] Richards, M. Fundamentals of Radar Signal Processing. 2nd ed. McGraw-Hill Professional Engineering, 2014.
[2] Richards, M., J. Scheer, and W. Holm. Principles of Modern Radar: Basic Principles. SciTech Publishing, 2010.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
This System object supports single and double precision for input data, properties, and arguments. If the input data
Xis single precision, the output data is single precision. If the input dataXis double precision, the output data is double precision. The precision of the output is independent of the precision of the properties and other arguments.
Version History
Introduced in R2017a
See Also
Functions
Objects
phased.DopplerEstimator|phased.RangeResponse|phased.RangeDopplerResponse|phased.CFARDetector|phased.CFARDetector2D
Topics
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)