Robot Dynamics
This topic details the different elements, properties, and equations of rigid body robot
dynamics. Robot dynamics are the relationship between the forces
acting on a robot and the resulting motion of the robot. In Robotics System Toolbox™, manipulator dynamics information is contained within a rigidBodyTree object, which specifies the rigid bodies, attachment points, and
inertial parameters for both kinematics and dynamics calculations.
Note
To use dynamics object functions, you must set the DataFormat property of the
rigidBodyTree object to
"row" or "column". These setting accept inputs
and return outputs as row or column vectors, respectively, for relevant robotics
calculations, such as robot configurations or joint torques.
Dynamics Properties
When working with robot dynamics, specify the information for individual bodies of
your manipulator robot using these properties of the rigidBody objects:
Mass— Mass of the rigid body in kilograms.CenterOfMass— Center of mass position of the rigid body, specified as a vector of the form[x y z]. The vector describes the location of the center of mass of the rigid body, relative to the body frame, in meters. ThecenterOfMassobject function uses these rigid body property values when computing the center of mass of a robot.Inertia— Inertia of the rigid body, specified as a vector of the form[Ixx Iyy Izz Iyz Ixz Ixy]. The vector is relative to the body frame in kilogram square meters. The inertia tensor is a positive definite matrix of the form: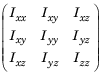
The first three elements of the
Inertiavector are the moment of inertia, which are the diagonal elements of the inertia tensor. The last three elements are the product of inertia, which are the off-diagonal elements of the inertia tensor.
For information related to the entire manipulator robot model, specify these rigidBodyTree object properties:
Gravity— Gravitational acceleration experienced by the robot, specified as an[x y z]vector in m/s2. By default, there is no gravitational acceleration.DataFormat— The input and output data format for the kinematics and dynamics functions, specified as"struct","row", or"column".
Dynamics Equations
Manipulator rigid body dynamics are governed by this equation:
also written as:
where:
— is a joint-space mass matrix based on the current robot configuration. Calculate this matrix by using the
massMatrixobject function.— are the Coriolis terms, which are multiplied by to calculate the velocity product. Calculate the velocity product by using by the
velocityProductobject function.— is the gravity torques and forces required for all joints to maintain their positions in the specified gravity
Gravity. Calculate the gravity torque by using thegravityTorqueobject function.— is the geometric Jacobian for the specified joint configuration. Calculate the geometric Jacobian by using the
geometricJacobianobject function.— is a matrix of the external forces applied to the rigid body. Generate external forces by using the
externalForceobject function.— are the joint torques and forces applied directly as a vector to each joint.
— are the joint configuration, joint velocities, and joint accelerations, respectively, as individual vectors. For revolute joints, specify values in radians, rad/s, and rad/s2, respectively. For prismatic joints, specify in meters, m/s, and m/s2.
To compute the dynamics directly, use the forwardDynamics object function. The function calculates the joint
accelerations for the specified combinations of the above inputs.
To achieve a certain set of motions, use the inverseDynamics object function. The function calculates the joint
torques required to achieve the specified configuration, velocities, accelerations, and
external forces.
See Also
Functions
forwardDynamics|inverseDynamics|externalForce|geometricJacobian|gravityTorque|centerOfMass|massMatrix|velocityProduct