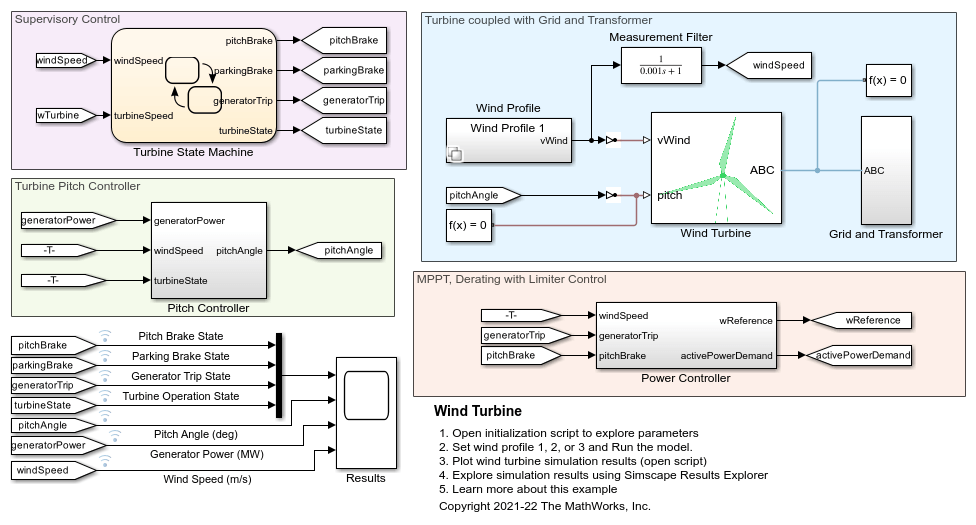
Wind Turbine

Turbine that converts wind motion into electrical energy

• Library:

• Simscape / Driveline / Engines & Motors

• 

Description

The Wind Turbine block represents a wind turbine that converts wind motion into mechanical rotational energy. You specify the incident wind velocity and collective blade pitch as inputs, and you can optionally output the thrust acting on the turbine. The block calculates the coefficients of power and torque using a table lookup such that

$$\begin{array}{l}{C}_P=tablelookup\left({\beta }_{Ref},{\lambda }_{Ref},C_{P,Ref},\beta ,{\lambda }_{Smooth},\text{interpolation = linear,extrapolation = nearest}\right)\\ C_T=tablelookup\left({\beta }_{Ref},{\lambda }_{Ref},C_{T,Ref},\beta ,{\lambda }_{Smooth},\text{interpolation = linear,extrapolation = nearest}\right)\end{array}$$

where:

• β_Ref is the reference pitch angle.

• λ_Ref is the reference tip speed ratio.

• C_P,Ref and C_T,Ref are the Power coefficient table and Thrust coefficient table parameters, respectively.

• λ_Smooth is the smoothed tip speed ratio.

The block uses this equation as the basis for the instantaneous tip speed ratio

$$\lambda =\frac{R\omega }{V},$$

where:

• R is the Turbine radius parameter.

• ɷ is the differential angular velocity between the shaft and the case.

• V is the incident air velocity on the rotor. This value is the physical signal input port V.

The block uses this equation to describe the smoothed version of the instantaneous tip speed ratio equation

$${\lambda }_{Smooth}=\frac{R\omega V}{\left(V^2+V_{Thr}^2\right)},$$

where V_Thr is the Velocity threshold parameter. The block uses these equations as a basis for the power and thrust

$$\begin{array}{l}Power=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.C_P\rho A{V}^3=Torque\cdot \omega \\ Thrust=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.C_T\rho A{V}^2\end{array}$$

where:

• ρ is the Air density parameter.

• A is the area of the circle swept by the turbine blades, and A = πr²

To relate the block parameters to the wind turbine mechanical power rating, determine the wind turbine power at the peak power coefficient and the rated wind speed. The rated power corresponds to the block parameters using this equation

$$Powe{r}_{rated}=0.5C_{P,max}\rho A{V}_{rated}^3,$$

where:

• C_P,max is the peak power coefficient. This is the maximum value in the Power coefficient table, Cp(β,TSR) parameter.

• V_rated is the rated wind speed. Rated wind speeds are typically 10 to 15 m/s. Wind turbine controller designs may alter strategy at this wind speed to maintain the rated power.

• A is the rotor swept area, where A = πr².

The block uses numerically smoothed equations for the thrust, power, and torque, such that

$$\begin{array}{l}Powe{r}_{Smooth}=\frac{C_P\rho A{\left(V^2+V_{thr}^2\right)}^{3/2}}{2}\\ Torqu{e}_{Smooth}=\frac{Powe{r}_{Smooth}}{\sqrt{{\omega }^2+{\left(V_{Thr}/R\right)}^2}}\\ Thrus{t}_{Smooth}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.C_T\rho AV\sqrt{V^2+V_{Thr}^2}\end{array}$$

When Rɷ < V_Thr, the block smoothly saturates the power to a near-zero threshold proportional to V_Thr³

Assumptions and Limitations

The block generates torque and power only for positive angular velocities.

Ports

Inputs

V — Incident wind velocity, m/s

physical signal

Physical signal input associated with the incident wind velocity, in m/s.

β — Pitch angle, deg

physical signal

Physical signal input associated with the pitch angle of the turbine blades, in deg.

Outputs

T — Thrust, N

physical signal

Physical signal output port associated with the axial force that the wind applies to the turbine blades, in N.

Dependencies

To enable this port, select Model thrust.

Conserving

R — Turbine shaft

mechanical rotational

Mechanical rotational conserving port associated with the wind turbine shaft.

C — Turbine casing

mechanical rotational

Mechanical rotational conserving port associated with the wind turbine casing.

Parameters

Model thrust — Turbine thrust output option

off (default) | on

Whether to model the thrust forces that the turbine encounters. Selecting this parameter enables port T.

Turbine radius — Blade tip radius

80 m (default) | positive scalar

Distance from the turbine hub center to the blade tips.

Pitch angle vector, β — Reference pitch angle

[0, 3, 5, 10, 20, 90] deg (default) | vector of length M

Reference collective blade pitch angle. The length of this vector defines the number of rows is the Power coefficient table, Cp(β,TSR) and Thrust coefficient table, Ct(β,TSR) parameters.

Tip speed ratio vector, TSR — Reference tip speed ratio

[0, 2, 4, 6, 8, 10, 12, 14, 15] (default) | vector of length N

Reference tip speed ratio (TSR). TSR is the ratio of the blade tip speed to wind speed. The length of this vector defines the number of columns in the Power coefficient table, Cp(β,TSR) and Thrust coefficient table, Ct(β,TSR) parameters. The block supports negative TSR values. The values must be strictly monotonically increasing.

Power coefficient table, Cp(β,TSR) — Power coefficient table

M-by-N matrix

Power coefficients for a given pitch angle and tip speed ratio. Each row corresponds to an element in the Pitch angle vector, β parameter, and each column corresponds to an element in the Tip speed ratio vector, TSR parameter. The default parameter value is [0.0000, 0.0161, 0.1446, 0.3865, 0.5009, 0.4404, 0.2545, 0.0002, -0.1384; 0.0016, 0.0173, 0.1079, 0.2676, 0.3779, 0.4111, 0.3838, 0.3176, 0.2753; 0.0027, 0.0197, 0.1151, 0.2606, 0.3469, 0.3558, 0.3069, 0.2222, 0.1718; 0.0054, 0.0283, 0.1315, 0.2364, 0.2589, 0.2022, 0.0929, -0.0455, -0.1204; 0.0109, 0.0536, 0.1320, 0.1256, 0.0120, -0.1752, -0.4017, -0.6435, -0.7655; -0.01 * ones(1, 9)].

Thrust coefficient table, Ct(β,TSR) — Thrust coefficient table

M-by-N matrix

Thrust coefficients for a given pitch angle and tip speed ratio. Each row corresponds to an element in the Pitch angle vector, β parameter, and each column corresponds to an element in the Tip speed ratio vector, TSR parameter. The default parameter value is [0.0000, 0.2451, 0.6740, 0.9616, 1.0000, 0.9882, 0.8430, 0.0002, -0.1341; 0.0016, 0.2541, 0.5942, 0.8582, 0.9561, 0.9754, 0.9599, 0.9092, 0.8669; 0.0027, 0.2705, 0.6113, 0.8503, 0.9339, 0.9407, 0.8993, 0.8016, 0.7239; 0.0054, 0.3215, 0.6475, 0.8205, 0.8482, 0.7727, 0.5565, -0.0450, -0.1171; 0.2035, 0.4335, 0.6485, 0.6348, 0.2129, -0.1684, -0.3701, -0.5712, -0.6681; -0.05 * ones(1, 9)] .

Dependencies

To enable this parameter, select Model thrust.

Air density — Air density

1.225 kg/m^3 (default) | positive scalar

Constant density of air.

Velocity threshold — Velocity smoothing threshold

0.01 m/s (default) | positive scalar

Threshold velocity smoothing location. This parameter smooths the torque, thrust, and power when the rotational speed approaches or crosses 0. The block applies more smoothing over greater velocity ranges as you increase the value of this parameter.

Model Examples

Wind Turbine

Model, parameterize, and test a wind turbine with a supervisory, pitch angle, MPPT (maximum power point tracking), and derating control. When you run the plot function, it generates a plot of the state transitions, normalized physical quantities such as the wind speed, wind turbine rotation speed, generator power, and pitch angle.

Open Model

References

[1] Manwell, J. F., J. G. McGowan, and A. L. Rogers. Wind Energy Explained: Theory, Design and Application. 1st ed. Wiley, 2009. https://doi.org/10.1002/9781119994367.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2022b