Cross Spectrum and Magnitude-Squared Coherence
This example shows how to use the cross spectrum to obtain the phase lag between sinusoidal components in a bivariate time series. The example also uses the magnitude-squared coherence to identify significant frequency-domain correlation at the sine wave frequencies.
Create the bivariate time series. The individual series consist of two sine waves with frequencies of 100 and 200 Hz. The series are embedded in additive white Gaussian noise and sampled at 1 kHz. The sine waves in the x-series both have amplitudes equal to 1. The 100 Hz sine wave in the y-series has amplitude 0.5, and the 200 Hz sine wave in the y-series has amplitude 0.35. The 100 Hz and 200 Hz sine waves in the y-series are phase-lagged by radians and radians, respectively. You can think of the y-series as the noise-corrupted output of a linear system with input x. Set the random number generator to the default settings for reproducible results.
rng default
Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x = cos(2*pi*100*t) + sin(2*pi*200*t) + 0.5*randn(size(t));
y = 0.5*cos(2*pi*100*t - pi/4) + 0.35*sin(2*pi*200*t - pi/2) + 0.5*randn(size(t));Obtain the magnitude-squared coherence estimate for the bivariate time series. The magnitude-squared coherence enables you to identify significant frequency-domain correlation between the two time series. Phase estimates in the cross spectrum are only useful where significant frequency-domain correlation exists.
To prevent obtaining a magnitude-squared coherence estimate that is identically 1 for all frequencies, you must use an averaged coherence estimator. Both Welch's overlapped segment averaging (WOSA) and multitaper techniques are appropriate. mscohere implements a WOSA estimator.
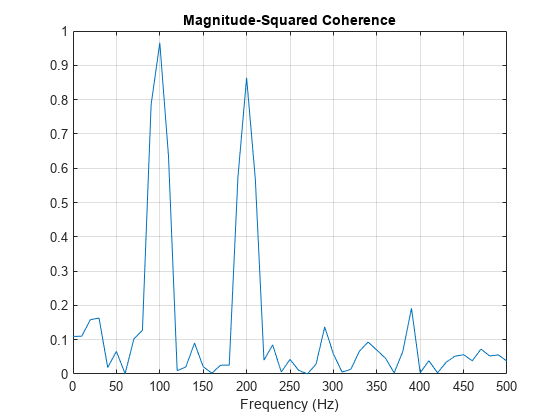
Set the window length to 100 samples. This window length contains 10 periods of the 100 Hz sine wave and 20 periods of the 200 Hz sine wave. Use an overlap of 80 samples with the default Hamming window. Input the sample rate explicitly to get the output frequencies in Hz. Plot the magnitude-squared coherence. The magnitude-squared coherence is greater than 0.8 at 100 and 200 Hz.
[Cxy,F] = mscohere(x,y,hamming(100),80,100,Fs); plot(F,Cxy) title('Magnitude-Squared Coherence') xlabel('Frequency (Hz)') grid
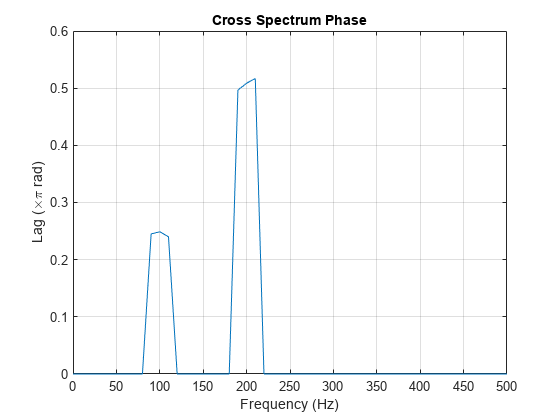
Obtain the cross spectrum of x and y using cpsd. Use the same parameters to obtain the cross spectrum that you used in the coherence estimate. Neglect the cross spectrum when the coherence is small. Plot the phase of the cross spectrum and indicate the frequencies with significant coherence between the two times. Mark the known phase lags between the sinusoidal components. At 100 Hz and 200 Hz, the phase lags estimated from the cross spectrum are close to the true values.
[Pxy,F] = cpsd(x,y,hamming(100),80,100,Fs); Pxy(Cxy < 0.2) = 0; plot(F,angle(Pxy)/pi) title('Cross Spectrum Phase') xlabel('Frequency (Hz)') ylabel('Lag (\times\pi rad)') grid