Two Cylinder Model with Load Constraints
This example shows how to model a rigid rod supporting a large mass interconnecting two hydraulic actuators. The model eliminates the springs as it applies the piston forces directly to the load. These forces balance the gravitational force and result in both linear and rotational displacement.
See two related examples that use the same basic components: four cylinder model and single cylinder model.
Note: This is a basic hydraulics example. You can more easily build hydraulic and automotive models using Simscape™ Driveline™ and Simscape Fluids™.
Simscape Fluids provides component libraries for modeling and simulating fluid systems. It includes models of pumps, valves, actuators, pipelines, and heat exchangers. You can use these components to develop fluid power systems such as front-loader, power steering, and landing gear actuation systems. Engine cooling and fuel supply systems can also be developed with Simscape Fluids. You can integrate mechanical, electrical, thermal, and other systems using components available within the Simscape product family.
Simscape Driveline provides component libraries for modeling and simulating one-dimensional mechanical systems. It includes models of rotational and translational components, such as worm gears, planetary gears, lead screws, and clutches. You can use these components to model the transmission of mechanical power in helicopter drivetrains, industrial machinery, vehicle powertrains, and other applications. Automotive components, such as engines, tires, transmissions, and torque converters, are also included.
Analysis and Physics of the Model
We assume the rotation angle of the rod is small. The equations of motion for the rod are given below in Equation Block 1. The equations describing the cylinder and pump behavior are the same as in the single cylinder example.
Equation Block 1:
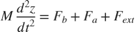
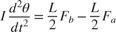




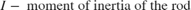
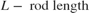
The positions and velocities of the individual pistons follow directly from the geometry. See the corresponding equations below in Equation Block 2.
Equation Block 2:
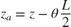
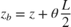
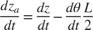
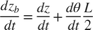

Opening the Model and Running the Simulation
To open this model, type sldemo_hydrod into the MATLAB® Command Window (click the hyperlink if you are using MATLAB Help). To run the simulation, on the Simulation tab, press Run. The model:
Logs signal data to the MATLAB workspace in the
Simulink.SimulationOutputobjectout. The signal logging data is stored inout, in aSimulink.SimulationData.Datasetobject calledsldemo_hydrod_output.
Logs continuous states data to MATLAB workspace. The states data is also contained in the
outworkspace variable, as a structure calledxout. Each state is assigned a name in the model to facilitate working with logged data. The names of the states are available in thestateNamefield ofxout.signals. For more information, see Data Format for Logged Simulation Data.
Uses the customizable Circular Gauge and Vertical Gauge blocks to visualize the fluid flow, pressure, and linear displacement in the cylinders.

Figure 1: Two cylinder model and simulation results
'Mechanical Load' Subsystem
This subsystem is shown in Figure 2. It solves the equations of motion, which we compute directly using standard Simulink blocks. It is assumed that the rotation angle is small. Look under the mask of the 'Mechanical Load' subsystem to see its structure (right-click on the subsystem and select Mask > Look Under Mask).

Figure 2: 'Mechanical Load' subsystem
Simulation Parameters
The parameters used in this simulation are identical to the parameters used in the single cylinder model, except for the following:
L = 1.5 m M = 2500 kg I = 100 kg/m^2 Qmax = 0.005 m^3/sec (constant) C2 = 3e-9 m^3/sec/Pa Fext = -9.81*M Newtons
Although the pump flow is constant, the model controls the valves independently. Initially, at t = 0, the cross-section of valve B is zero. It grows linearly to 1.2e-5 m^2 at t = 0.01 sec, and then linearly decreases to zero at t = 0.02 sec. The cross-section of valve A is 1.2e-5 sq.m. at t = 0 and it linearly decreases to zero at t = 0.01 sec, then it linearly increases to 1.2e-5 sq.m. at t = 0.02 sec. Then the behavior of the valves A and B repeats periodically with the same pattern. In other words the valves A and B are 180 degrees out of phase.
Results
Figures 3 and 4 show the linear and angular displacements of the rod. The linear displacement response is typical of a type-one integrating system. The relative positions and the angular movement of the rod illustrate the response of the two pistons to the out-of-phase control signals (the cross-section of the valves A and B).

Figure 3: Linear displacement of the pistons and the load (load is in the middle of the rod)

Figure 4: Angular displacement of the rod
Close Model
Close the model and clear all generated data.
Conclusions
Simulink provides a productive environment for simulating hydraulic systems, offering enhancements that provide enormous productivity in modeling and flexibility in numerical methods. The use of masked subsystems and model libraries facilitates structured modeling with automatic component updates. As users modify library elements, the models that use the elements automatically incorporate the new versions. Simulink can use differential-algebraic equations (DAEs) to model some fluid elements as incompressible and others as compliant, allowing efficient solutions for complex systems of interdependent circuits.
Models such as this one can ultimately be used as part of overall plant or vehicle systems. The hierarchical nature of Simulink allows independently developed hydraulic actuators to be placed, as appropriate, in larger system models (for example adding controls in the form of sensors or valves). In cases such as these, tools from the Control System Toolbox™ can analyze and tune the overall closed-loop system. The MATLAB/Simulink environment can thus support the entire design, analysis, and modeling cycle.
