General Applications
Simulink® allows you to model and simulate a wide range of dynamic systems. These example models illustrate a variety of general applications, from simple to complex.
Featured Examples
Simulation of Bouncing Ball
Uses two models of a bouncing ball to show different approaches to modeling hybrid dynamic systems with Zeno behavior. Zeno behavior is informally characterized by an infinite number of events occurring in a finite time interval for certain hybrid systems. As the ball loses energy, the ball collides with the ground in successively smaller intervals of time.
Analyze Impact of Model Parameters on Bouncing Ball Simulation
Analyzes the impact of the damping coefficient on a mass-spring-damper model of the dynamics of a bouncing ball. After running a simulation using a vectorized parameter value, the example analyzes the effect of varying the parameter by exploring these questions:
Single Hydraulic Cylinder Simulation
Use Simulink® to model a hydraulic cylinder. You can apply these concepts to applications where you need to model hydraulic behavior.
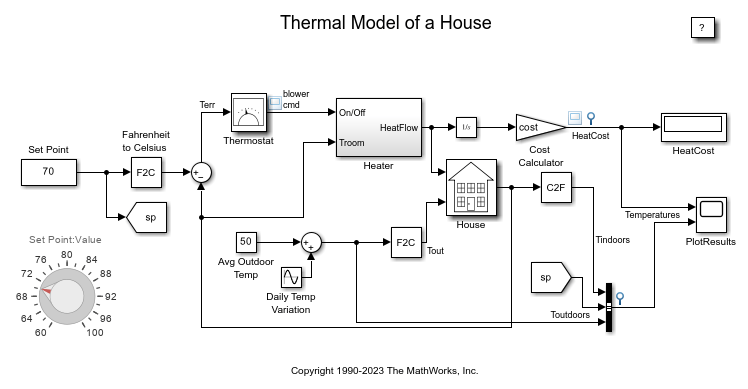
Thermal Model of a House
Use Simulink® to create the thermal model of a house. This system models the outdoor environment, the thermal characteristics of the house, and the house heating system.
Approximating Nonlinear Relationships: Type S Thermocouple
Approximate nonlinear relationships of a type S thermocouple.
Digital Waveform Generation: Approximate a Sine Wave
Design and evaluate a sine wave data table for use in digital waveform synthesis applications in embedded systems and arbitrary waveform generation instruments.
Accurate Zero-Crossing Detection
How zero-crossing detection works in Simulink®. Simulink uses zero-crossing detection to accurately simulate an abrupt model change or discontinuity without decreasing the solver time steps. For more information, see Zero-Crossing Detection.
Spiral Galaxy Formation Simulation Using MATLAB Function Blocks
Use MATLAB Function blocks to simulate and plot galaxy interactions.
Counters Using Conditionally Executed Subsystems
Implement counters using Enabled and Triggered subsystems. In this example, the model sldemo_counters controls flow of water into a tank and uses a counter to count the number of times overflow occurs, where overflow occurs when the water level in the tank is 8 meters or more for 30 seconds or more.
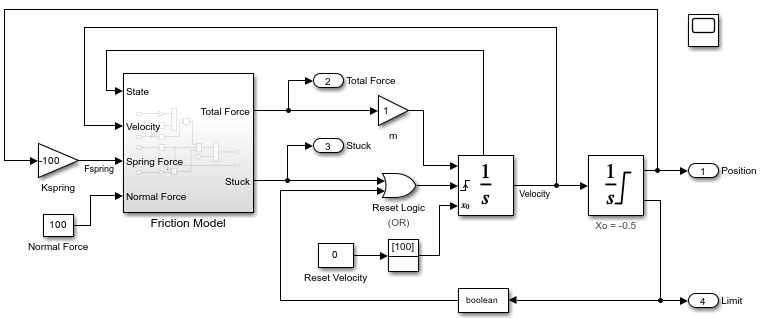
Model Stick-Slip Friction and Hard Stops in Mass-Spring-Damper System
One way you can incorporate hard stops and friction changes from stick-slip motion into a mass-spring-damper model.
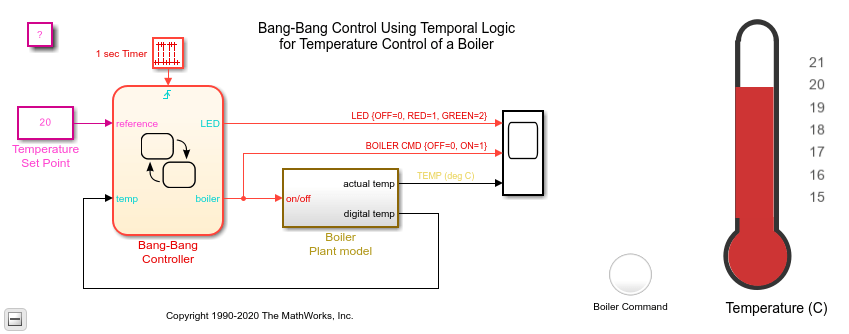
Bang-Bang Control Using Temporal Logic
Use Stateflow® to model a bang-bang temperature control system for a boiler. The boiler dynamics are modeled in Simulink®.
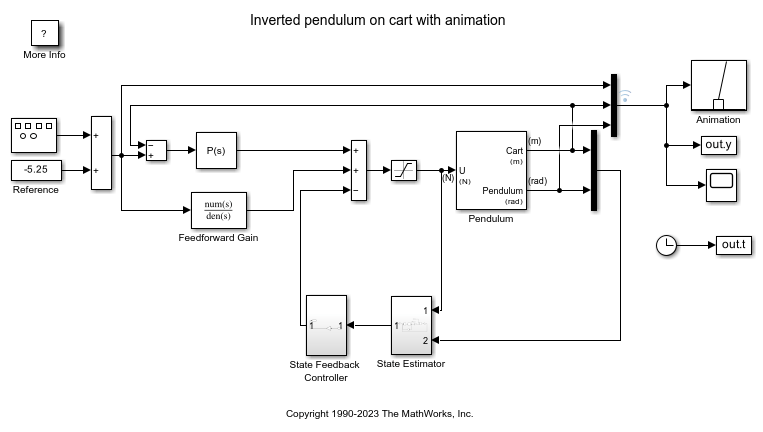
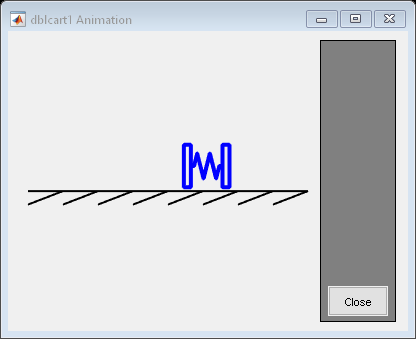
Inverted Pendulum with Animation
Use Simulink® to model and animate an inverted pendulum system. An inverted pendulum has its center of mass above its pivot point. To stably maintain this position, the system implements control logic to move the pivot point below the center-of mass as the pendulum starts to fall. The inverted pendulum is a classic dynamics problem used to test control strategies.
Double Spring Mass System
Model a double spring-mass-damper system with a periodically varying forcing function. The model uses an S-Function block to animate the mass system during simulation. In the system, the only sensor is attached to the mass on the left, and the actuator is attached to the mass on the left. The example uses state estimation and linear-quadratic regulator (LQR) control.
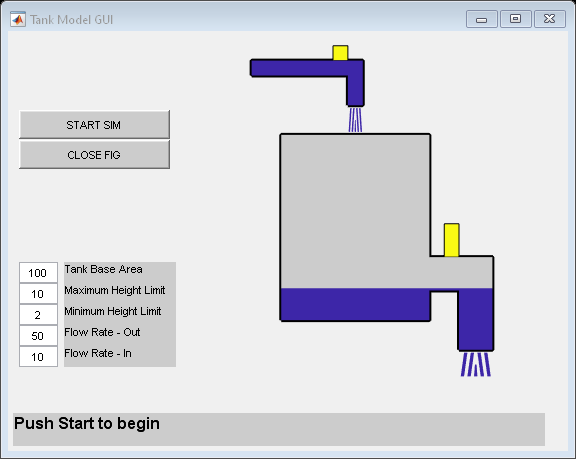
Tank Fill and Empty with Animation
Model the dynamics of liquid in a tank. The model simulates liquid inflow and outflow.
Simulating Systems with Variable Transport Delay Phenomena
Two cases where you can use Simulink® to model variable transport delay phenomena.
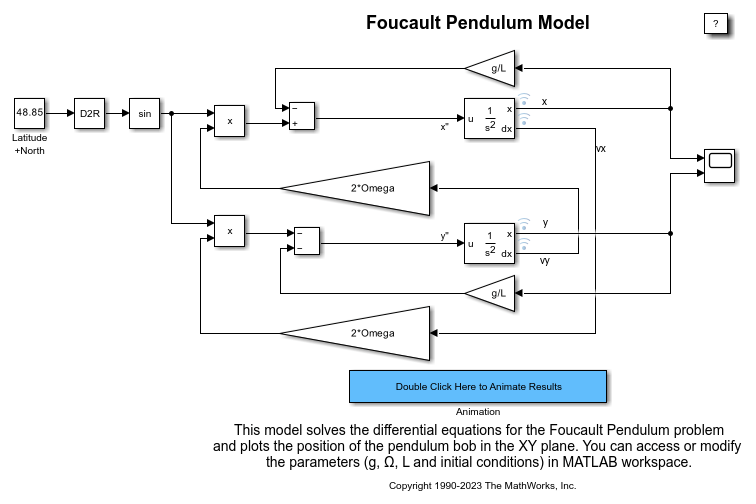
Foucault Pendulum Model
Model a Foucault pendulum. The Foucault pendulum was the brainchild of the French physicist Leon Foucault. It was intended to prove that Earth rotates around its axis. The oscillation plane of a Foucault pendulum rotates throughout the day as a result of axial rotation of the Earth. The plane of oscillation completes a whole circle in a time interval T, which depends on the geographical latitude.
Foucault Pendulum Model with Simulink 3D Animation
Animate the Foucault Pendulum Model in the Simulink® 3D Animation™ environment. You can modify the pendulum location by changing the Latitude constant values in the model and other parameters in MATLAB® workspace.
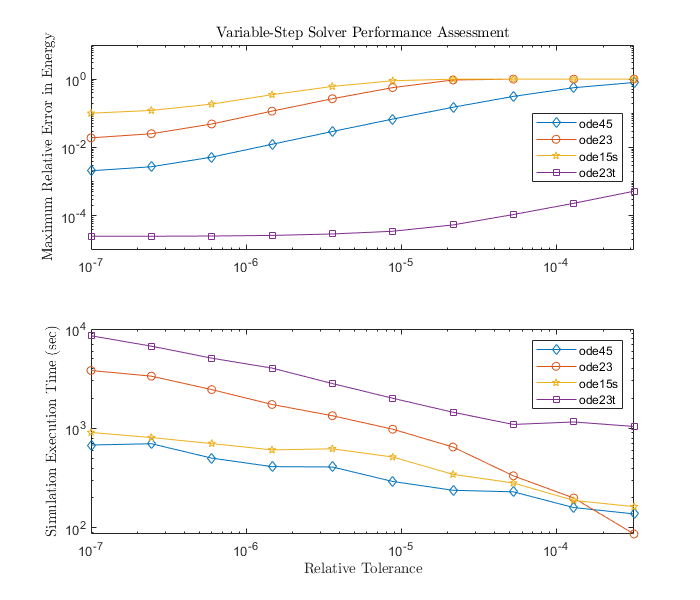
Explore Variable-Step Solvers with Stiff Model
The behavior of variable-step solvers in a Foucault pendulum model. Simulink® solvers ode45, ode15s, ode23, and ode23t are used as test cases. Stiff differential equations are used to solve this problem. There is no exact definition of stiffness for equations. Some numerical methods are unstable when used to solve stiff equations and very small step sizes are required to obtain a numerically stable solution to a stiff problem. A stiff problem may have a fast changing component and a slow changing component.
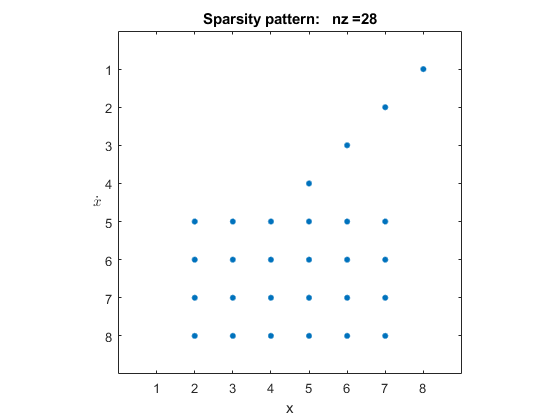
Exploring the Solver Jacobian Structure of a Model
The example shows how to use Simulink® to explore the solver Jacobian sparsity pattern, and the connection between the solver Jacobian sparsity pattern and the dependency between components of a physical system. A Simulink model that models the synchronization of three metronomes placed on a free moving base are used.
Double Bouncing Ball: Use of Adaptive Zero-Crossing Location
Choose the correct zero-crossing location algorithm, based on the system dynamics. For Zeno dynamic systems, or systems with strong chattering, you can select the adaptive zero-crossing detection algorithm through the Configure pane:
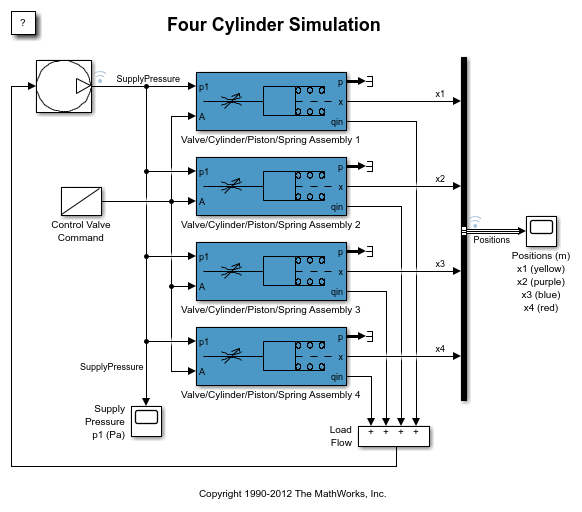
Four Hydraulic Cylinder Simulation
Use Simulink to create a model with four hydraulic cylinders. The model has a single pump and four actuators.
Two Cylinder Model with Load Constraints
Use Simulink to model a rigid rod supporting a large mass interconnecting two hydraulic actuators. This model eliminates the springs as it applies the piston forces directly to the load.
Power Analysis of Spring-Mass-Damper System
Analyze mechanical power of mass-spring damper system.
Van der Pol Oscillator
Model the second-order Van der Pol (VDP) differential equation in Simulink®. In dynamics, the VDP oscillator is non-conservative and has nonlinear damping. At high amplitudes, the oscillator dissipates energy. At low amplitudes, the oscillator generates energy. The oscillator is given by this second-order differential equation:
Collision Avoidance and Trajectory Tracking of a Marine Vessel
Follow a pre-defined trajectory and avoid collisions.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)