Double Bouncing Ball: Use of Adaptive Zero-Crossing Location
This example shows how to choose the correct zero-crossing location algorithm, based on the system dynamics. For Zeno dynamic systems, or systems with strong chattering, you can select the adaptive zero-crossing detection algorithm through the Configure pane:
--> Solver
--> Zero-crossing options
--> Algorithm: [Nonadaptive, Adaptive]The Double Bouncing Ball System
The Simulink® model in this example is used to simulate two bouncing balls. They start from the ground with different initial speeds, and their ground levels will change at different times.
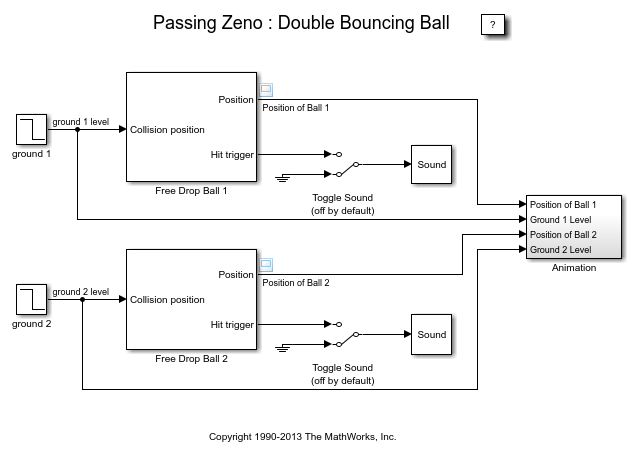

Figure 1: The double bouncing ball model and animation
Double Bouncing Balls with Non-adaptive Zero-Crossing Location Algorithm
If the Non-adaptive zero-crossing location algorithm is used, the consecutive zero-crossing error causes the simulation to stop. This system is actually a 'Zeno dynamic system'. When either ball is very close to the ground, Simulink will stop responding because too many zero crossings are detected in a very short period.

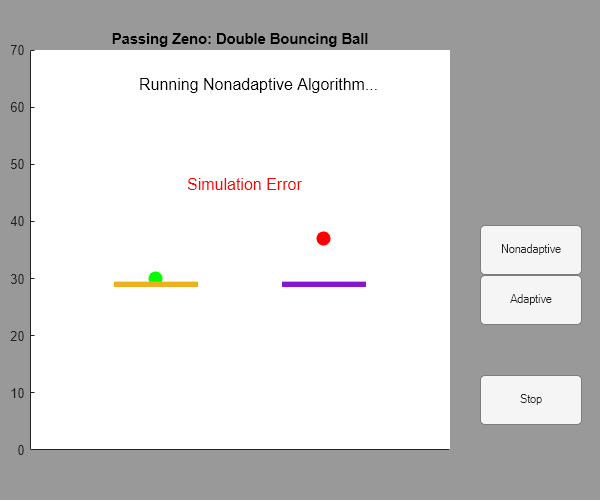
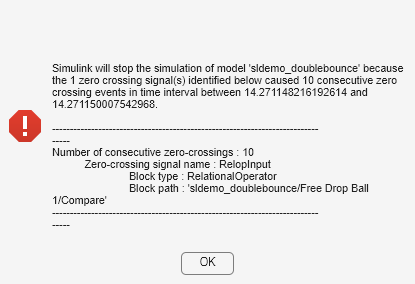
Figure 2: Vertical displacement of both balls with Non-adaptive zero- crossing location algorithm.
The simulation does not complete and an error message is shown. The ground level changing events cannot be observed.
Double Bouncing Balls with Adaptive Zero-Crossing Location Algorithm
If the adaptive algorithm is selected, Simulink will adaptively turn on/off the process to precisely locate the zero-crossing time. The conditions to turn on/off the location are:
1) Zero-crossing signal value is below a threshold value. You can control the threshold value through the Configure pane:
--> Solver
--> Zero-crossing options
--> Algorithm: [Adaptive]
--> Signal threshold2) Consecutive zero-crossing diagnostic is hit. You can define consecutive zero crossing through the Configure pane:
--> Solver
--> Solver diagnostic controls
--> Time tolerance and
--> Number of consecutive zero crossings.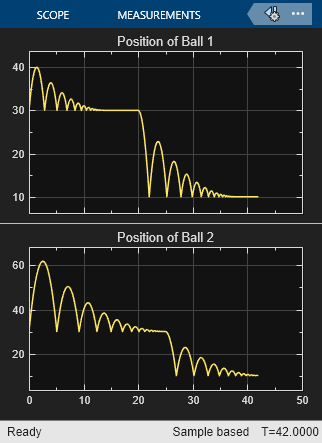

Figure 3: Vertical displacement of both balls with adaptive zero crossing location algorithm.
The simulation has completed. The ground level changing events can be observed. A warning is shown to inform you when searching for events is turned off.