fixpt_look1_func_plot
Plot fixed-point approximation function for lookup table
Syntax
fixpt_look1_func_plot(xdata,ydata,'func',...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth)
errworst = fixpt_look1_func_plot(xdata,ydata,'func',...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth)
Description
fixpt_look1_func_plot( plots
a lookup table approximation function and the error from the ideal
function.xdata,ydata,'func',...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth)
errworst = fixpt_look1_func_plot(xdata,ydata,'func',...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth)errworst is the maximum
absolute error.
You can use fixpt_look1_func_approx to
generate xdata and ydata,
the breakpoints and table data for the lookup table, respectively. fixpt_look1_func_approx applies the
ideal function to the breakpoints in xdata to
produce ydata. While this method is the
easiest way to generate ydata, you can
choose other values for ydata as input
for fixpt_look1_func_plot. Choosing different
values for ydata can, in some cases, produce
a lookup table with a smaller maximum absolute error.
Input Arguments
| Vector of breakpoints for the lookup table. | ||||||||
| Vector of values from applying the ideal function to the breakpoints. | ||||||||
| Function of | ||||||||
| Minimum value of | ||||||||
| Maximum value of | ||||||||
| Data type of | ||||||||
| Scaling for the | ||||||||
| Data type of | ||||||||
| Scaling for the | ||||||||
| Rounding mode supported by fixed-point Simulink® blocks:
|
Examples
Plot a fixed-point approximation
of the sine function using data points generated by fixpt_look1_func_approx:
func = 'sin(2*pi*x)'; % Define the range over which to optimize breakpoints xmin = 0; xmax = 0.25; % Define the data type and scaling for the inputs xdt = ufix(16); xscale = 2^-16; % Define the data type and scaling for the outputs ydt = sfix(16); yscale = 2^-14; % Specify the rounding method rndmeth = 'Floor'; % Define the maximum acceptable error errmax = 2^-10; % Choose even, power-of-2 spacing for breakpoints spacing = 'pow2'; % Generate data points for the lookup table [xdata,ydata,errworst]=fixpt_look1_func_approx(func,... xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,[],spacing); % Plot the sine function (ideal and fixed-point) & errors fixpt_look1_func_plot(xdata,ydata,func,xmin,xmax,... xdt,xscale,ydt,yscale,rndmeth);
fixpt_look1_func_plot plots
the fixed-point sine function, using generated data points, and plots
the error between the ideal function and the fixed-point function.
The maximum absolute error and the number of points required appear
on the plot. The error drops to zero at a breakpoint, but increases
between breakpoints due to curvature differences between the ideal
function and the line drawn between breakpoints.
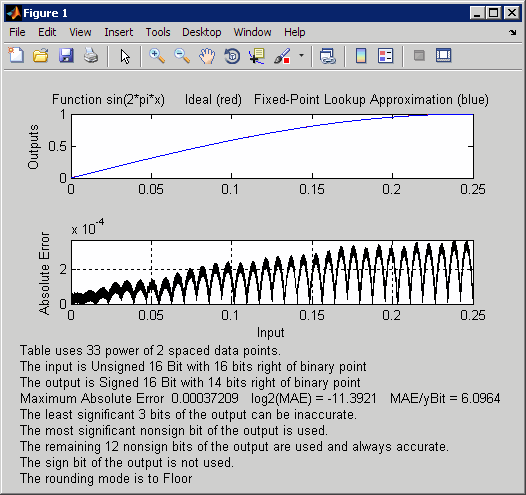
The lookup table requires 33 points to achieve
a maximum absolute error of 2^-11.3922.
Version History
Introduced before R2006a
See Also
fixpt_evenspace_cleanup | fixpt_look1_func_approx
Topics
- Producing Lookup Table Data (Fixed-Point Designer)
- Use Lookup Table Approximation Functions (Fixed-Point Designer)