Improve Simulation Performance by Using Local Solvers
This example shows how using a local solver can speed up simulations of model hierarchies that contain components that operate on different time scales. The model in this example simulates the step response of a DC motor that drives a mechanical load.

In the DC motor model used in this example, the electrical physics of the motor operate on a much faster time scale than the resulting mechanical motion. When you use referenced models to represent system components, you can configure one or more of the referenced models that represent each system component to use a local solver. This example analyzes the performance benefit of using a local solver for the electrical model of the DC motor.
Analyze System Dynamics
To determine whether your system might benefit from using a local solver, analyze the dynamics of your system. Consider using local solvers to improve simulation performance when:
The dynamics of one or more components are much faster or slower compared to the dynamics of other components in the system.
The solver best suited for the overall system is not ideal or well suited for one or more components.
Open the model DCMotorLocalSolver. The model implements the system using two referenced models:
The model
DCMotorElectricalmodels the electrical response of the motor.The model
DCMotorMechanicalmodels the mechanical response of the motor.
The electrical and mechanical models are coupled by the motor current and the angular speed of the motor and load. The block diagram represents the coupling using signals that connect the model references in the top model.
mdltop = "DCMotorLocalSolver";
open_system(mdltop)
To analyze the electrical component, open the referenced model named DCMotorElectrical in the Simulink® Editor by double-clicking the Model block named Electrical. Alternatively, open the model in the context of the model hierarchy by using a Simulink.BlockPath object.
mdlblkelec = mdltop + "/Electrical";
elecblk = Simulink.BlockPath(mdlblkelec);
open(elecblk)
The electrical response of the motor is modeled as a series RL circuit. Using Kirchoff's Voltage Law, you can express the input voltage as the sum of the voltage on the motor resistance , the voltage on the motor inductance , and the voltage due to the motor electrical constant and the angular velocity .
The electrical model of the motor calculates the value of the current, which the mechanical system uses to calculate the speed of the motor and load. Rearrange the equation to match the implementation in the model.
The motor inductance and resistance determine the electrical time constant of the motor.
The motor in this example has an inductance of 2.5 and a resistance of 3 , which results in an electrical time constant of approximately 800 ns.
To analyze the mechanical component, navigate back to the top model by clicking the back arrow ![]() . Then, open the referenced model named
. Then, open the referenced model named DCMotorMechanical in the Simulink Editor by double-clicking the Model block named Mechanical. Alternatively, open the model in the context of the model hierarchy by using a Simulink.BlockPath object.
mdlblkmech = mdltop + "/Mechanical";
mechblk = Simulink.BlockPath(mdlblkmech);
open(mechblk)
The mechanical component models the rotational motion that results from the torque produced by the motor current. The total rotational moment of inertia from the motor and the load times the angular acceleration is equal to the sum of the forces in the system. The motor current and the magnetic field in the armature coil create a force scaled by the motor torque constant . For this example, assume the magnetic field is constant. The angular speed creates a force that is scaled by the viscous friction of the motor .
The mechanical model of the motor integrates the angular acceleration to calculate the angular speed of the motor and load, which the electrical system uses to calculate the current.
The motor resistance, the inertia of the motor and load, the electrical constant, and the torque constant for the motor determine the mechanical time constant [1].
The motor in this model has a resistance of 3 , an electrical constant of 0.025 , and a torque constant of 0.25 . The total moment of inertia for the system is 3.2 , resulting in a mechanical time constant of approximately 15 ms.
The Model DCMotorLocalSolver can likely benefit from using local solvers because the dynamics of the electrical component, which has a time constant of 800 ns, differ significantly, by several orders of magnitude, from the dynamics of the mechanical component, which has a time constant of 15 ms.
Run Baseline Simulation
To confirm that using a local solver for the electrical component improves simulation performance without affecting the simulation results more than desired, create a baseline for the outputs and timing of a simulation that uses a single solver.
When you simulate the model using a single solver, the whole system must run using the same time step. Because the electrical time constant is much smaller than the mechanical time constant, the dynamics of the electrical component constrain the choice of the step size. The step size must be small enough to capture the dynamics of the electrical response.
For this example, the model uses the fixed-step solver ode3 with a step size of 200 ns. Before running the baseline simulation, ensure that neither referenced model uses a local solver by disabling the UseModelRefSolver parameter of each referenced model.
set_param(mdltop,SolverType="Fixed-step",Solver="ode3",FixedStep="2e-7") mechmdl = "DCMotorMechanical"; set_param(mechmdl,UseModelRefSolver="off") elecmdl = "DCMotorElectrical"; set_param(elecmdl,UseModelRefSolver="off")
Simulate the model to create a baseline for the simulation results and execution time.
baseout = sim(mdltop);
To see the amount of time required to execute the simulation, check the ExecutionElaspedWallTime field of the TimingInfo structure in the simulation metadata. The Simulink.SimulationOutput object baseout contains a Simulink.SimulationMetadata object with information about the model and simulation, including the structure TimingInfo. When you simulate the entire system using the ode3 solver with a step size of 200 ns, the execution phase of the simulation runs for several seconds.
exbase = baseout.SimulationMetadata.TimingInfo.ExecutionElapsedWallTime
exbase = 6.6633
To capture a baseline for the simulation results, the Record block in the model logs the position and speed data to the Simulation Data Inspector. Access the run created in the Simulation Data Inspector and change the name to Baseline: DCMotorLocalSolver.
baserun = Simulink.sdi.Run.getLatest;
baserun.Name = "Baseline";Simulate Using Local Solver
To see the performance benefit and impact on the model outputs, configure the electrical model to use a local solver. When the electrical model uses a local solver, the top solver for the model DCMotorLocalSolver does not need to consider the dynamics of the electrical system. Only the much larger mechanical time constant and the communication step size, which specifies the rate at which the top and local solvers exchange data, constrain the top solver step size. The top solver can take much larger steps and compute results for many fewer time steps in the simulation, which can improve simulation performance.
Configure the top solver to use a step size of 2 ms.
set_param(mdltop,FixedStep="2e-3")Configure the model DCMotorElectrical to use the solver ode3 as a local solver with a step size of 200 ns. You can specify the configuration parameters of the referenced model from the top model, by using the Property Inspector or the Block Parameters dialog box.
Open the Property Inspector. On the Modeling tab, expand the Design section and select Property Inspector, or press Ctrl+Shift+I.
To open the Configuration Parameters dialog box for the referenced model, select the Model block named
Electrical. Then, in the Property Inspector, expand the Solver section, and click the hyperlink next to the Use local solver parameter.Configure the model to use a local solver when referenced in a model hierarchy. In the Configuration Parameters dialog box for the model
DCMotorElectrical, on the Model Referencing pane, select Use local solver when referencing model.Select the fixed-step solver
ode3as the local solver. In the Configuration Parameters dialog box, on the Solver pane, from the Type list, selectFixed-step. Then, from the Solver list, selectode3 (Bogacki-Shampine).Set the local solver step size to 200ns. On the Solver pane, expand Solver details. Then, in the Fixed-step size (fundamental sample time) box, enter
2e-7.Apply the settings to the model. In the Configuration Parameters dialog box, click OK.
Alternatively, you can specify the configuration parameters of the referenced model programmatically using the set_param function.
elecmdl = "DCMotorElectrical"; set_param(elecmdl, ... UseModelRefSolver="on", ... SolverType="Fixed-step", ... Solver="ode3", ... FixedStep="2e-7");
In the top model, the Model block that references the electrical model of the motor indicates that the referenced model uses a local solver by displaying the name of the selected solver on the block icon.

Finally, specify the communication step size for the Model block that references the electrical model of the motor. The communication step size specifies when the parent and local solvers exchange data. The value you choose might affect the accuracy of the simulation results.
The communication step size must be an integer multiple of both the parent solver step size and the local solver step size. For this example, set the communication step size for the Model block named Electrical to the smallest possible value of 2 ms, equal to the top solver step size.
commstep = "2e-3";
set_param(mdlblkelec,CommunicationStepSize=commstep)When the local solver uses zero-order hold output signal handling, the communication step size also defines the discrete sample time the Model block propagates to its output ports. Because the component with faster dynamics uses the local solver in this example, only zero-order hold output signal handling is supported. To prevent warnings about sample time discrepancies across the model reference interface for the mechanical component, set the sample time of the input port in the model DCMotorMechanical.
outPort = mechmdl + "/Current";
set_param(outPort,SampleTime=commstep)Simulate the model using the local solver to simulate the electrical model of the motor.
localout = sim(mdltop);
Check the simulation metadata to see the amount of time the simulation spent in the execution phase. When you use a local solver for the much faster electrical dynamics, the simulation runs much faster, spending less than a second in the execution phase compared to several seconds with a single solver.
exlocal = localout.SimulationMetadata.TimingInfo.ExecutionElapsedWallTime
exlocal = 3.3413
Calculate the performance improvement as a percentage of the baseline simulation execution time.
pctimprovement = (exbase - exlocal)/exbase * 100
pctimprovement = 49.8543
Access the run created in the Simulation Data Inspector. Change the name to Local Solver: DCMotorLocalSolver.
localrun = Simulink.sdi.Run.getLatest;
localrun.Name = "LocalSolver";Analyze Simulation Results
To see whether using a local solver affected the simulation results, plot the position and speed data from both simulations in the Simulation Data Inspector. On the Simulation tab, under Review Results, click Data Inspector.
Alternatively, open the Simulation Data Inspector using the Simulink.sdi.view function.
Simulink.sdi.view
In the Simulation Data Inspector, plot the speed and position signals from the two runs. Alternatively, use the Simulink.sdi.loadView function to load the view named DCMotorLocalSolver1, which was created for this example.
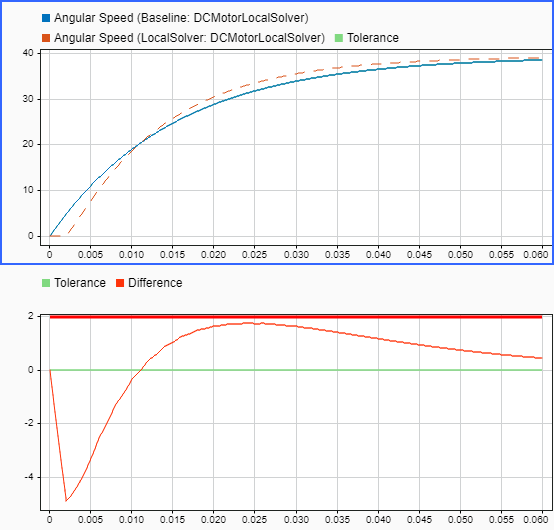
Simulink.sdi.loadView("DCMotorLocalSolver1.mldatx");The results from the local solver simulation are nearly the same as the results from the baseline simulation that used a single solver. The solid line shows the baseline result. The dotted line shows the local solver result.

The biggest difference occurs in the Angular Speed signal at the start of the simulation. The local solver results start to match the single solver results more closely after the first major time hit that corresponds to the communication step size, which is the first time top solver receives updated information from the local solver about the electrical response.
To evaluate whether the configuration of the local solver satisfies accuracy requirements, compare the runs using the Simulation Data Inspector.
To navigate to the Compare pane in the Simulation Data Inspector, click Compare.
From the Baseline list, select
Baseline: DCMotorLocalSolver.From the Compare to list, select
LocalSolver: DCMotorLocalSolver.To run the comparison, click Compare.
Alternatively, compare the runs programmatically using the Simulink.sdi.compareRuns function.
compresults = Simulink.sdi.compareRuns(baserun.ID,localrun.ID);
The comparison results indicate that neither signal matches within the default tolerance of 0 between the baseline simulation and the simulation that used the local solver. The table in the Simulation Data Inspector shows that the maximum difference computed for the angular speed signals is much larger than the maximum difference computed for the angular position signals.

To view plots of the angular speed signals and the computed difference signal, select the row in the table for the angular speed signals. The plot of the difference signal shows that the maximum difference occurs at the start of the simulation and that the difference in the signal value is significantly smaller than the maximum difference for most of the simulation.
When you have specific accuracy requirements for your system, you can incorporate those requirements into the comparison by specifying a combination of absolute, relative, and time tolerance values for the comparison.
Several aspects of the local solver configuration can affect the accuracy of the simulation results. Because the local solver in this example uses a step size that is smaller than the communication step size, the only option available to improve the simulation results is decreasing the communication step size. However, in this example, decreasing the communication step size requires also decreasing the top solver step size, which results in a smaller performance improvement.
Reference
[1] Younkin, George W. "Electric Servo Motor Equations and Time Constants." https://support.controltechnologycorp.com/customer/elearning/younkin/driveMotorEquations.pdf.