Simulink Models
A model is an abstract and simplified description of a system using mathematical equations and diagrams. The modeling concepts in this topic provide context for understanding the process of mathematically describing a system with Simulink® software tools.
Block Diagram
A block diagram is a visual representation of a model in the Simulink Editor. The editor allows you to add blocks selected from block libraries representing elementary model components. Elementary components include integrator, gain, and sum blocks. Blocks are connected to each other with signal and event lines to visually construct the model equations.
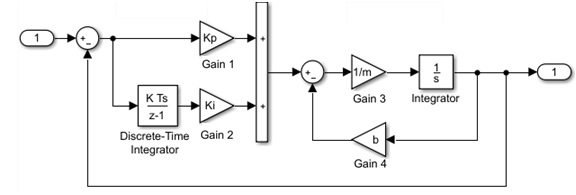
Block Diagram Semantics
A classic block diagram of a system is drawn graphically with blocks and lines. The history of these block diagrams is derived from engineering areas such as Feedback Control Theory and Signal Processing. A block within a block diagram defines a model in itself. The relationships between elementary models are represented by signal lines connecting the blocks. The blocks and lines in a block diagram collectively describe the overall model of a system.

Simulink extends classic block diagrams by:
Adding a set of equations (block methods) to each block that defines the time-based relationships between the input signals, output signals, and block state variables.
Adding parameters to each block that specify the coefficients from the model equations.
Providing an engine for numerical solution of the block diagram by evaluating the relationships over time, where time starts at a user-specified “start time” and ends at a user-specified “stop time.”
See also: Simulink Block Diagrams, Simulation.
Blocks
A block is a basic modeling construct of the Simulink Editor. Add blocks from the built-in Simulink libraries to perform specific operations. You can also create custom blocks. Some blocks have input signals, output signals, and states. Most blocks have parameters that you use to specify block behavior. Whether a block has parameters and the nature of those parameters is specific to each block.

Each block represents a set of equations for the Simulink engine. The equations are represented as block methods. The blocks shown above have the following block methods.

Block methods are evaluated during the simulation of a block diagram. The evaluation of the block methods is performed within a simulation loop, where each cycle through the simulation loop represents the evaluation of the block diagram at a given point in time.
Virtual Blocks
Virtual blocks organize and provide graphical hierarchy in a model. During model simulation, Simulink expands the blocks in place before execution, a process known as flattening. This expansion is similar to the way macros work in a programming language such as C or C++.
Simulink defines the following virtual blocks:
Virtual Subsystem – Use a virtual subsystem to encapsulate related and functional parts within a larger model. A Virtual Subsystem block has the check box for the parameter Treat as atomic unit cleared.

Inport and Outport – Use port blocks to move data (signals) and events (function calls) from outside a Subsystem block or Model block to within the block, and vice versa.

Bus Creator, Bus Assignment, Bus Selector – Bus blocks combine signals into a virtual bus and manage the routing of signals around a complex block diagram. Virtual buses are a graphical convenience and do not change the behavior of the model.

See Nonvirtual and Virtual Blocks, Signal Types, Composite Interface Guidelines.
Nonvirtual Blocks
Nonvirtual blocks provide execution control and graphical hierarchy in a model. Simulink defines the following nonvirtual Subsystem and Model blocks:
Atomic Subsystem and Model – Blocks within an Atomic Subsystem block or a Model block that references a model execute as a single unit (atomic execution) at each time step. For an Atomic Subsystem block, the check box for the parameter Treat as atomic unit is selected.
You can place any Simulink block in an Atomic Subsystem or referenced model, including blocks with different execution rates. This flexibility provides the advantage of grouping functional aspects of a model at the execution level.
In the following example, the vehicle model is an Atomic Subsystem block containing blocks that model the mechanics of a car. The control model is referenced from a Model block.

Enabled and/or Triggered – Atomic Subsystem or Model block whose execution is controlled by external data from a signal. Contains an Enable or Trigger block, or both. For the Trigger block, the parameter Trigger type is set to
rising,falling, oreither.
Function-Call – Atomic Subsystem or Model block whose execution is controlled by an event from a function-call initiator (such as a Stateflow® chart or a Function-Call Generator, S-Function, or Hit Crossing block). Contains a Trigger block with Trigger type set to
function-call.
Simulink defines the following nonvirtual components only for Subsystem blocks.
Action Subsystem – Atomic Subsystem block whose execution is controlled by an event from an action initiator (e.g., If or Switch Case block). Contains an Action Port block within the Subsystem block.

While Iterator Subsystem – Atomic Subsystem block that runs multiple iterations during each model time step. Contains a While Iterator block that controls the number of iterations by evaluating a logical condition.
A while iterator subsystem is similar to a function-call subsystem in that it can run for any number of iterations at a given time step. The while iterator subsystem differs from a function-call subsystem in that there is no separate initiator.
For Iterator Subsystem – Atomic Subsystem block that runs a fixed number of iterations during each model time step. Contains a For Iterator block that controls the number of iterations.
Block Mask
A block mask is a custom block parameter interface that displays only selected block parameters. A mask for a Subsystem block allows you to provide an interface for setting parameters on blocks inside the Subsystem block without having to navigate the model hierarchy.
See Masking Fundamentals.
Custom Blocks
Custom blocks are new blocks that extend the built-in functionality of Simulink. You can create libraries of custom blocks to use in your model.
The following blocks define the algorithm of a custom block either graphically with a block diagram or programmatically:
MATLAB® Function – Code a MATLAB function using the MATLAB language that runs in a Simulink model. See Implement MATLAB Functions in Simulink with MATLAB Function Blocks.
MATLAB System – Bring existing
Systemobjects based onmatlab.Systeminto Simulink. See Create Custom Blocks Using MATLAB System Block and System objects.Subsystem – Draw a block diagram representing an algorithm, wrap this diagram in an instance of the Simulink Subsystem block, then provide the block with a parameter dialog box using a Simulink block mask. See Subsystem.
C Caller – Integrate your external C code into a Simulink model. See Integrate C Code Using C Caller Blocks.
S-Function – Create a custom block programmatically by creating a MATLAB file or a MEX file that contains the block's system functions. The resulting file is called an S-function. You then associate the S-function with instances of the Simulink S-Function block in your model. See S-Function.
Lines
A line is a basic modeling construct of the Simulink Editor. Lines connect the output ports of blocks with the input ports of other blocks.
Signal Lines
Signal lines transfer data during a simulation from one block to another block. Signals are time-varying quantities that have values at all points in time (continuous) or at specified time points (discrete). The source of a signal corresponds to the block that writes to the signal during evaluation of its block output method. The destination of a signal is the block that reads the signal during the evaluation of its block input method.
You can specify signal attributes, including signal name, data type (e.g., double, 32-bit integer), numeric type (e.g., real, complex) and dimension (e.g., one-dimensional, two-dimensional, multi-dimension array). Many blocks can accept or output a signal of any data type or dimensionality. Other blocks impose restrictions on the attributes of the signals they can handle.
During a simulation, save data from a signal by logging the signals.

Event Lines
In response to a function-call or action initiator, event lines send an event to a Subsystem or Model block. The block that receives the event executes the blocks within it one or more times during a time step. Function-call initiators include Stateflow charts, Function-Call Generator blocks, S-Function blocks, and Hit Crossing blocks. Action initiators include If and Switch Case blocks.

See Signals and Signal Basics.
Message Lines
A message line indicates a path along which a message can advance within a distributed system. Messages are used to model asynchronous event-based communication between Simulink components for the purpose of system integration.
A message output port provides a way for the block to send a message. Conversely, a message input port provides a way for the block to receive the message. You can use message lines to connect blocks from Stateflow chart, Simulink Message and Event library.

Data
Data includes the parameter and input signal values that Simulink uses to produce the output values resulting from simulating the behavior of a model.
Types of data:
Model parameters – Variables to specify block and signal parameters in a model. Includes MATLAB variables, parameter and signal data objects, data type objects, and bus objects.
Model configuration parameters – Parameters that determine how your model runs by specifying the settings that control model behavior.
Simulation data – Input data to drive a simulation and output data generated by a simulation.
Data Objects – Instances of data classes that allow you to specify characteristics of signals, states, and block parameters. Use the
Simulink.SignalandSimulink.Parameterclasses to create data objects. See Data Objects.
Location of data:
Block parameters – Use block parameters to directly specify numerical values. You can also enter a variable name and define its value in the Simulink model workspace, a Simulink data dictionary, or the MATLAB base workspace.

MATLAB base workspace – Use the MATLAB base workspace to save variables that are separate from the model in a MAT file or MATLAB script.

Simulink treats the base workspace and the data dictionary as a single global name space. If the base workspace and a referenced data dictionary have identical variable names, Simulink uses the variable value in the data dictionary.
The MATLAB base workspace contains variables that are global and visible to all Simulink models.

See Comparison of Signal Loading Techniques, Save Simulation Data.
Simulink model workspace – Use the model workspace to define and store local data variables. Variables defined in a model workspace are visible only within the scope of the model with a unique name space. Therefore, you can use the same variable name in multiple model workspaces and you can assign a unique variable value to the name in each model.

Define variables in the data dictionary using Model Explorer. In the Modeling tab, click Model Explorer
 . In the left pane, select Model
Workspace.
. In the left pane, select Model
Workspace.
Values for the model workspace variables are initialized from values saved with the model, from a separate MAT file or MATLAB file, or using MATLAB code saved with the model.
See Model Workspaces, Specify Source for Data in Model Workspace.
Simulink data dictionary – Use a data dictionary to define and store global data, share data between models, and track changes made to the data. Data is saved in a file separate from the model.

Create a data dictionary file. In the Modeling tab, under Design, click Data Dictionary
 . Click New and enter a
file name with an extension
. Click New and enter a
file name with an extension .sldd.
Define variables in the data dictionary using Model Explorer. In the Modeling tab, click Model Explorer
 . In the left pane, select Design
Data.
. In the left pane, select Design
Data.
Imported and exported data – Import signals for a simulation from the MATLAB base workspace, a MAT file, or a spreadsheet. Create input signals using a source block or the Signal Editor block. Use signal logging to export simulation results. Signals are saved as vectors
[t, X, Y]for time, state and output at each major time step.
See also: Determine Where to Store Variables and Objects for Simulink Models, Symbol Resolution.
Parameters
Parameters are Simulink model characteristics that affect the simulation and code generation result.
Model Configuration Parameters
Model configuration parameters specify model behavior during compilation, simulation, and code generation, such as the solver to use and the types of errors and warnings to display.
To specify model configuration parameters, in the Modeling tab, click Model Settings. The Configuration Parameters dialog box opens.

Block Parameters
Block parameters define model dynamics and mathematics. Whether a block has parameters that you can set and the nature of those parameters is specific to each block. To specify block parameters, open the block parameter dialog box, or in the Modeling tab, under Design, click one of the following:
Property Inspector – Specify block parameters directly or enter a variable name for a parameter value.
Model Data Editor – Specify block parameters with variables.
Model Explorer – Specify block parameters with variables.
Block Parameter Variables
If you have a single parameter used in many locations across a large model, updating every instance of that parameter can be a difficult task. Instead, enter a variable name as the value of a parameter, then define the variable once using one of the following methods:
Simulink Model Workspace – Create model workspace variables and assign values to the variables. The parameters you define are specific to the model and saved with the model. Use a MATLAB variable for ease of maintenance. Use a
Simulink.Parameterobject to control additional properties including data type, dimensions, and units. See Edit and Manage Workspace Variables by Using Model Explorer.Simulink Data Dictionary – Create design data variables in a data dictionary and link the dictionary to a model. During model simulation, Simulink retrieves data from the data dictionary.
MATLAB Base Workspace – In the MATLAB base workspace, define parameters using any MATLAB mechanism for defining a variable. For example, you can use a MAT file and load the variables when you open the model. Use MATLAB expressions to specify parameter variable values. Simulink evaluates the expressions before running a simulation. See Save and Load Workspace Variables.
Using the MATLAB base workspace or a Simulink data dictionary to define variables is useful when you are using the same set of parameters for more than one model. This mechanism also allows you to use different sets of parameter values for the same model.
See also: Share and Reuse Block Parameter Values by Creating Variables, Create, Edit, and Manage Workspace Variables.
Model Argument and Instance Parameters
When you reference the same model from multiple Model blocks, you create instances of the model. You can set block parameters to use the same value or a different value for each instance of the model.
To use different values,
In the model workspace for the referenced model, create a MATLAB variable or
Simulink.Parameterobject.Enter a parameter name and a default parameter Value. Select the Argument check box to create a model argument.
For a block in the referenced model, enter the name of the model argument for the value of a block parameter.
For each Model block, open the block parameters dialog box, select the Instance parameters tab, and enter a value for the instance parameter with the model argument name.
See also: Configure Instance-Specific Values for Block Parameters in a Referenced Model.
Tunable Block Parameters
You can change the value of a tunable block parameter during a simulation. This allows you to determine interactively the most suitable value for a parameter. When you change the value of a tunable parameter, the change takes effect at the start of the next time step. For example, the gain parameter of the Gain block is tunable. You can change the block gain while a simulation is running. See Tune and Experiment with Block Parameter Values.
Setting Block Parameters with the Property Inspector
To specify parameters, in the Modeling tab, under Design, click Property Inspector. Click a block to display the block parameters and properties.

See also: Specify Block Properties.
Properties
Properties are Simulink model characteristics that generally do not affect the simulation result. To specify properties, in the Modeling tab, under Design, click Property Inspector.
Model Properties
With the Property Inspector opened, click a blank space within a block diagram, or in the Modeling tab, select Model Settings > Model Properties. Model properties include:
General – Name and location of model file.
Design Data – Variables defined outside the model that parameterize the model and its blocks and signals.
Callbacks – Commands that execute when a specific model event occurs.
Block Properties
With the Property Inspector opened, select a block, then select the Properties tab. Block properties include:
Block Annotation – Values of selected block parameters displayed below the block.
Callbacks – Commands that execute when a specific block event occurs. For example, you can set up a MATLAB script to load and define block parameter variables using expressions.
Priority – Set the relative execution order of blocks. A lower value executes the block before a larger priority value.
Tags – Block identifiers that are programmatically searchable.
Port Properties
With the Property Inspector opened, select a port, then select the Properties tab. You can modify properties of port objects, signals, and port blocks with the Property Inspector. The ports on a subsystem block also have a port block tab, which contains properties of the associated port block.

The port block properties are displayed for these subsystem blocks:
The ports on these blocks show a tab with the same name as the type of port block and list the properties that are shown in the Model Explorer window. For example, an EnablePort Block tab is shown for ports on an Enable block, and Data, Message, or Event tabs are shown for ports on Stateflow blocks.
Enable block
Trigger block
Function Call block
Reset block
Action Port block
Chart (Stateflow)
Truth Table (Stateflow)
State Transition Table (Stateflow)
Test Sequence (Simulink Test)
matlabFunctionBlock(Symbolic Math Toolbox)


The port properties of read-only blocks are not editable. For example, the port properties of locked linked library blocks, masked blocks, and protected referenced models are read-only.
The port block properties on Model blocks are shown only if the model is loaded.
Setting Model and Block Properties with Property Inspector
To set properties, in the Simulation tab, under Prepare, click Property Inspector. Click an empty space to display the model properties. Click a block to display the block properties.

See also: Specify Block Properties, Customize Model Behavior with Callbacks.
State variables
The state of a model is defined by the values of its state variables. State variables are the set of variables whose values at time zero, along with the values of model inputs and the model equations, can determine the behavior of a model during a simulation. Examples of state variables include motor position and velocity, inductor current, capacitor voltage, solution temperature, and gas pressure.
If the current output value of a block is a function of the previous output value, the block defines a state variable that needs to be saved between time steps. Computing a block output hence entails saving the value of the state variable at the current time step for use in computing the output at a subsequent time step.
Working with States
The following facilities are provided for determining, initializing, and logging model states during simulation:
The Data Import/Export pane of a model's Configuration Parameters dialog box (see Save Block States and Simulation Operating Points) allows you to specify initial values for model states, and to record the values of the states at each time step during simulation as an array or structure variable in the MATLAB workspace.
Open the Configuration Parameters dialog box. Select the States check block for logging to the MATLAB variable
xout.
In the MATLAB Command Window, list the logged values for state of the Integrator block at each time step.
>> xout{1}.Values.Data ans = 0.0000 1.8127 3.2968 4.5119 . . .You can use the name of a model as a programmatic interface to display information about the states defined by a model, including the total number of states and the block that defines each state with its initial value.
List blocks in the model
vehicle_modelwith states. In the MATLAB Command Window, enter the model function, then list blocks with states.[sys,x0,blks,ts] = vehicle_model([],[],[],'sizes'); blksblks = {'vehicle_model/Integrator'}The Simulink debugger displays the value of a state at each time step during a simulation, and the
statesfunction for the Simulink debugger displays information about the current states (see Debug Simulations Programmatically).In the MATLAB Command Window, start the Simulink debugger, then enter the command
states.sldebug 'vehicle_model' (sldebug @0): >> statesContinuous States for 'vehicle_model': Idx Value (system:block:element Name 'BlockName') 0. 0 (0:0:0 CSTATE 'vehicle_model/Integrator')Using the Block Parameters dialog box or the
get_paramfunction with theContinuousStateAttributesparameter, you can name states for blocks that have continuous states, such as the Integrator block. Naming states can simplify analyzing logged states data, especially when a block has multiple states.
Continuous States
A continuous state is defined for all values of time. An example of a continuous state would be the speed of a car shown on an analog speedometer with a needle position that changes continuously with the rotation of a tire.
Blocks with continuous states and the block parameter Initial condition include:
In general, excluding simple models, analytical methods do not exist for integrating states represented by ordinary differential equations. Integrating the states requires the use of numerical methods.
Discrete States
A discrete state is defined only at specific times. It is an approximation of a continuous state where the state is updated at periodic or aperiodic time intervals. An example of a discrete state would be the speed of a car shown on a digital speedometer that is updated every second as opposed to continuously.
Blocks with discrete states include:
Computing the discrete state for a block requires knowing its value at the previous time step and also the current input value to the block. Simulink provides two types of discrete solvers:
Fixed-step discrete solver – determines a fixed step size that hits all the sample times for all the model's discrete states, regardless of whether the states actually change value at the sample time hits.
Variable-step discrete solver – varies the step size to ensure that sample time hits occur only at times when the states change value.
Modeling Hybrid Systems
A hybrid model has both continuous and discrete states. Solving such a model entails choosing a step size that satisfies both the precision constraint on the continuous state integration and the sample time interval constraint on the discrete states. Simulink meets this requirement by passing the next sample time interval for the discrete solver as an additional constraint on the continuous solver. The continuous solver chooses a step size that advances the simulation up to but not beyond the time of the next discrete sample time. The continuous solver can take a time step short of the next sample time hit to meet its accuracy constraint but it cannot take a step beyond the next sample time hit even if its accuracy constraint allows it to.
You can simulate hybrid systems using any of the integration methods, but certain
methods are more effective than others. For most hybrid systems,
ode23 and ode45 are superior to the other
solvers in terms of efficiency. Because of discontinuities associated with the
sample and hold of the discrete blocks, do not use the ode15s and
ode113 solvers for hybrid systems.
Sample Time
Sample time is the time interval that specifies the rate (1 / sample time) for executing block methods to produce outputs and update the internal states of blocks. Time is an inherent component of a block diagram in that the simulation results of a block diagram change with time.
Sample time is specified as:
Continuous – Blocks run at variable times based on solver settings.
Discrete – Blocks run at specific times that are explicitly specified.
In the following example, the controller runs at a discrete rate specified with a
sample time of 0.01 seconds while Simulink determines the vehicle model to have a continuous sample time.

Determining a system's behavior over time thus entails repeatedly solving the model at intervals, called time steps or time intervals, from the start of the time span to the end of the time span. The process of solving a model at successive time steps is referred to as simulating the system that the model represents.
See also What Is Sample Time?, Types of Sample Time, Specify Sample Time, View Sample Time Information.
Block Sample Times
Every Simulink block has a sample time which defines when the block will execute.
Most blocks allow you to specify the sample time via a SampleTime
parameter. Common choices include discrete, continuous, and inherited sample
times.
| Common Sample Time Types | Sample Time | Examples |
|---|---|---|
| Discrete | [Ts,
To] | Unit Delay, Digital Filter |
| Continuous | [0, 0] | Integrator, Derivative |
| Inherited | [–1, 0] | Gain, Sum |
For discrete blocks, the sample time is a vector [Ts, To] where Ts is the time interval or period between consecutive sample times and To is an initial offset to the sample time. In contrast, the sample times for nondiscrete blocks are represented by ordered pairs that use zero, a negative integer, or infinity to represent a specific type of sample time. For example, continuous blocks have a nominal sample time of [0, 0] and are used to model systems in which the states change continuously (e.g., a car accelerating), whereas you indicate the sample time type of an inherited block symbolically as [–1, 0], and Simulink then determines the actual value based upon the context of the inherited block within the model.
Note that not all blocks accept all types of sample times. For example, a discrete block cannot accept a continuous sample time.
For a visual aid, Simulink allows the optional color-coding and annotation of any block diagram to indicate the type and speed of the block sample times. You can capture all of the colors and the annotations within a legend (see View Sample Time Information).
For a more detailed discussion of sample times, see Sample Time.
Units
Units are used to measure the total amount of a quantity.
Simulink units are specified as an Inport block or Outport block parameter at the boundaries of a Simulink model component. Simulink model components include Subsystem blocks, Model blocks, Stateflow charts, and Simulink to Simscape™ converter blocks. To display units on a model, in the Debug tab, select Information Overlays > Units.

See also: Unit Specification in Simulink Models, Converting Units.
Direct Feedthrough
Direct feedthrough is where the output port signal of a block is computed from the values of its input port signals. The output signal value is a function of the input signal values.
Blocks with direct feedthrough include the Gain, Product, Sum, and Math Function blocks.

Algebraic Loop
A signal loop between blocks with direct feedthrough is called an algebraic loop. An algebraic loop generally occurs when an input port of a block with direct feedthrough is driven directly by the output port of the same block or indirectly through other blocks with direct feedthrough.
In the following model, the two Gain blocks with direct feedthrough create an algebraic loop:

See also: Algebraic Loop Concepts.
Artificial Algebraic Loops
An artificial algebraic loop occurs when an atomic subsystem or Model block causes Simulink to detect an algebraic loop, even though the contents of the subsystem do not contain a direct feedthrough from the input to the output. When you create an atomic subsystem, all Inport blocks are direct feedthrough, resulting in an algebraic loop.
Start with the included model, which represents a simple proportional control of the plant described by
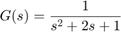
which can be rewritten in state-space form as
![$$ \dot{x} = \left[ \begin{array}{cc} -2 & -1 \\ 1 & 0 \end{array} \right] + \left( \begin{array}{c} 0\\1 \end{array} \right) $$](../../examples/simulink/win64/ArtifAlgLoopsExample_eq12603750421915334129.png)
![$$ y = \left[\begin{array}{cc}0&1\end{array}\right] $$](../../examples/simulink/win64/ArtifAlgLoopsExample_eq18346827941344727566.png)
The system has neither algebraic variables nor direct feedthrough and does not contain an algebraic loop.
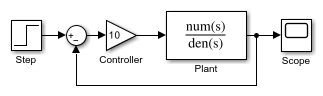
Modify the model as described in the following steps:
Enclose the Controller and Plant blocks in a subsystem.
In the subsystem dialog box, select Treat as atomic unit to make the subsystem atomic.
In the Diagnostics pane of the Model Configuration Parameters, set the Algebraic Loop parameter to
error.
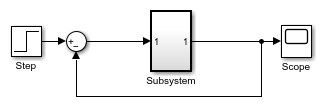
When simulating this model, an algebraic loop occurs because the subsystem is direct feedthrough, even though the path within the atomic subsystem is not direct feedthrough. Simulation stops with an algebraic loop error.
Zero-Crossing Detection
Simulink uses a technique known as zero-crossing detection to accurately locate a discontinuity without resorting to excessively small time steps during a simulation. Usually this technique improves simulation run times.