Battery
(To be removed) Generic battery model
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Sources
Description
The Battery block implements a generic dynamic model that represents most popular types of rechargeable batteries.
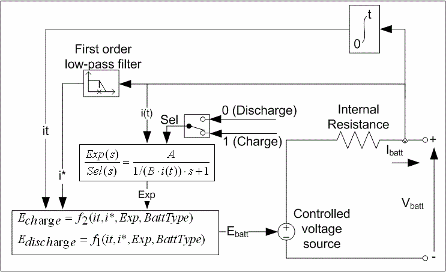
This figure shows the equivalent circuit that the block models.
Charge and Discharge Characteristics
The circuit parameters can be modified to represent a specific battery type and its discharge characteristics. A typical discharge curve consists of three sections.
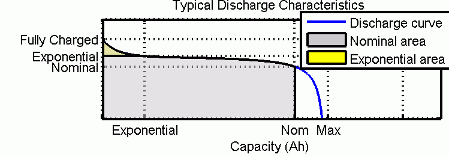
The first section represents the exponential voltage drop when the battery is charged. The width of the drop depends on the battery type. The second section represents the charge that can be extracted from the battery until the voltage drops below the battery nominal voltage. Finally, the third section represents the total discharge of the battery, when the voltage drops rapidly.
When the battery current is negative, the battery recharges, following a charge characteristic.

The model parameters are derived from the discharge characteristics. The discharging and charging characteristics are assumed to be the same.
The Exp(s) transfer function represents the hysteresis phenomenon for the lead-acid, nickel-cadmium (NiCD), and nickel-metal hydride (NiMH) batteries during the charge and discharge cycles. The exponential voltage increases when a battery is charging, regardless of the battery's state of charge. When the battery is discharging, the exponential voltage decreases immediately.

The state of charge (SOC) for a battery is a measure of battery's charge, expressed as a percent of the full charge. The depth of discharge (DOD) is the numerical complement of the SOC, such that DOD = 100% - SOC.
For example, if the SOC is:
100% — The battery is fully charged and the DOD is 0%.
75% — The battery is 3/4 charged and the DOD is 25%.
50% — The battery is 1/2 charged and the DOD is 50%.
0% — The battery is has 0 charge and the DOD is 100%.
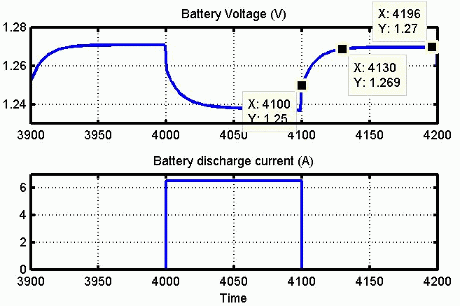
Model Validation
Experimental validation of the model shows a maximum error of 5% (when SOC is between 10% and 100%) for the charge (when the current is 0 through 2 C) and discharge (when the current is 0 through 5 C) dynamics.
Parameterization
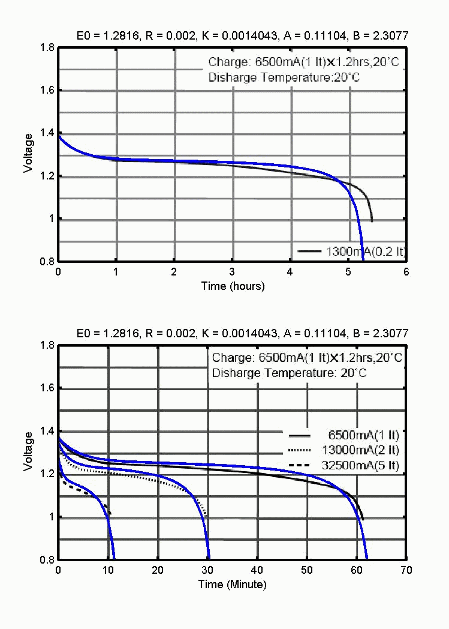
This figure shows detailed parameters extracted from the Panasonic NiMH-HHR650D battery data sheet.

You can obtain the rated capacity and the internal resistance from the specification tables. The other detailed parameters are derived from the Typical Discharge Characteristics plot.
Parameter | Value |
|---|---|
Rated Capacity |
|
Internal Resistance |
|
Nominal Voltage (a) |
|
Rated Capacity |
|
Maximum Capacity (b) |
|
Fully Charged Voltage (c) |
|
Nominal Discharge Current (d) |
|
Capacity @ Nominal Voltage (a) |
|
Exponential Voltage (e) |
|
Exponential Capacity (e) |
|
These parameters are approximate and depend on the precision of the points obtained from the discharge curve.
The discharge curves you obtain from these parameters, which are marked by dotted lines in the following figures, are similar to the data sheet curves.
To model a series and/or parallel combination of cells based on the parameters
of a single cell, use the parameter transformation shown in the following table
can be used. The Nb_ser variable corresponds to the number of
cells in series, and Nb_par corresponds to the number of
cells in parallel.
| Parameter | Value |
|---|---|
Nominal voltage | 1.18 * Nb_ser |
Rated capacity | 6.5 * Nb_par |
Maximum capacity | 7 * Nb_par |
Fully charged voltage | 1.39 * Nb_ser |
Nominal discharge current | 1.3 * Nb_par |
Internal resistance | 0.002 * Nb_ser/Nb_par |
Capacity at nominal voltage | 6.25 * Nb_par |
Exponential zone | 1.28 * Nb_ser, 1.3 * Nb_par |
Equations
For the lead-acid battery type, the model uses these equations.
Discharge Model (i* > 0)
Charge Model (i* < 0)
with it > 0 during charging.
For the lithium-ion battery type, the model uses these equations.
Discharge Model (i* > 0)
Charge Model (i* < 0)
For the nickel-cadmium and nickel-metal-hydride battery types, the model uses these equations.
Discharge Model (i* > 0)
Charge Model (i* < 0)
In the equations:
EBatt is the nonlinear voltage, in V.
E0 is the constant voltage, in V.
Exp(s) is the exponential zone dynamics, in V.
Sel(s) represents the battery mode. Sel(s) =
0during battery discharge, Sel(s) =1during battery charging.K is the polarization constant, in V/Ah, or polarization resistance, in Ohms.
i* is the low-frequency current dynamics, in A.
i is the battery current, in A.
it is the extracted capacity, in Ah.
Q is the maximum battery capacity, in Ah.
A is the exponential voltage, in V.
B is the exponential capacity, in Ah−1.
Limitations and Assumptions
Limitations
The minimum no-load battery voltage is 0 V and the maximum battery voltage is equal to 2 × E0.
The minimum capacity of the battery is 0 Ah and the maximum capacity is Qmax.
Assumptions
The internal resistance is assumed to be constant during the charge and discharge cycles and does not vary with the amplitude of the current.
The parameters of the model are derived from the discharge characteristics. The discharging and charging characteristics are assumed to be the same.
The capacity of the battery does not change with the amplitude of the current (there is no Peukert effect).
The self-discharge of the battery is not represented. It can be represented by adding a large resistance in parallel with the battery terminals.
The battery has no memory effect.
Ports
Output
Conserving
Parameters
References
[1] Omar N., M. A. Monem, Y. Firouz, J. Salminen, J. Smekens, O. Hegazy, H. Gaulous, G. Mulder, P. Van den Bossche, T. Coosemans, and J. Van Mierlo. “Lithium iron phosphate based battery — Assessment of the aging parameters and development of cycle life model.” Applied Energy, Vol. 113, January 2014, pp. 1575–1585.
[2] Saw, L.H., K. Somasundaram, Y. Ye, and A.A.O. Tay, “Electro-thermal analysis of Lithium Iron Phosphate battery for electric vehicles.” Journal of Power Sources. Vol. 249, pp. 231–238.
[3] Tremblay, O., L.A. Dessaint, "Experimental Validation of a Battery Dynamic Model for EV Applications." World Electric Vehicle Journal. Vol. 3, May 13–16, 2009.
[4] Zhu, C., X. Li, L. Song, and L. Xiang, “Development of a theoretically based thermal model for lithium ion battery pack.” Journal of Power Sources. Vol. 223, pp. 155–164.