PWM Generator (Three-phase, Three-level)
Generate three-phase, three-level pulse width modulated signal or waveform for gating switching devices
Libraries:
Simscape /
Electrical /
Control /
Pulse Width Modulation
Description
The PWM Generator (Three-phase, Three-level) block controls switching behavior for a three-phase, three-level power converter. The block:
Calculates on- and off-gating times based on the block inputs:
Three sinusoidal reference voltages
A DC-link voltage
A DC-link neutral point balance control signal
Uses the gating times to generate 12 switch-controlling pulses.
Uses the gating times to generate modulation waveforms.
Sampling Mode
This block allows you to choose natural, symmetric, or asymmetric sampling of the modulation wave.
The PWM Generator (Three-phase, Two-level) block does not perform carrier-based pulse width modulation (PWM). Instead, the block uses input signals to calculate gating times and then uses the gating times to generate both the switch-controlling pulses and the modulation waveforms that it outputs.
Carrier-based PWM is, however, useful for showing how the sampling mode that you select relates to the switch-on and switch-off behavior of the pulses that the block generates. A generator that uses a three-level, carrier-based PWM method:
Samples a reference wave.
Compares the sample to two parallel triangle carrier waves, separated by one level.

Generates a switch-on pulse if a sample is higher than the carrier signal or a switch-off pulse if a sample is lower than the carrier wave.
To determine switch-on and switch-off pulse behavior, a three-level carrier-based PWM generator uses these methods to sample each of the triangle waves:
Natural — The sampling and comparison occur at the intersection points of the modulation wave and the carrier wave.

Asymmetric — Sampling occurs at the upper and lower boundaries of the carrier wave. The comparison occurs at the intersection that follows the sampling.

Symmetric — Sampling occurs only at the upper boundary of the carrier wave. The comparison occurs at the intersection that follows the sampling.

Overmodulation
The modulation index, which measures the ability of the power converter to output a given voltage, is defined as
where
m is the modulation index.
Vm is the peak value of the modulation wave.
Vc is the peak value of the triangle carrier wave.

For three-phase SPWM,
where
Vpeak is the peak value of the fundamental component of the phase-to-neutral voltage.
vdc is the DC-link voltage.
For three-phase space-vector PWM (SVM),
For normal steady-state operation, 0 <m ≤
1. If a transient, such as a load increase, causes the
amplitude of Vm to exceed the amplitude of
Vc, overmodulation
(m > 1) occurs
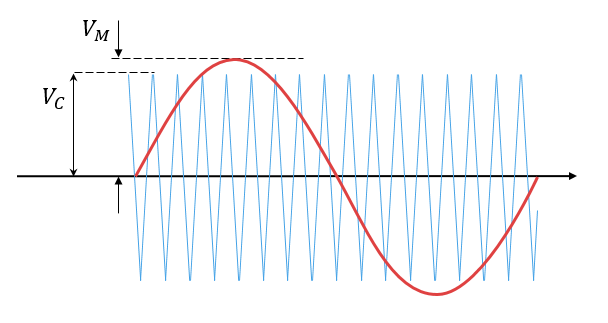
If overmodulation occurs, the output voltage of the power converter clamps to the positive or negative DC rail.
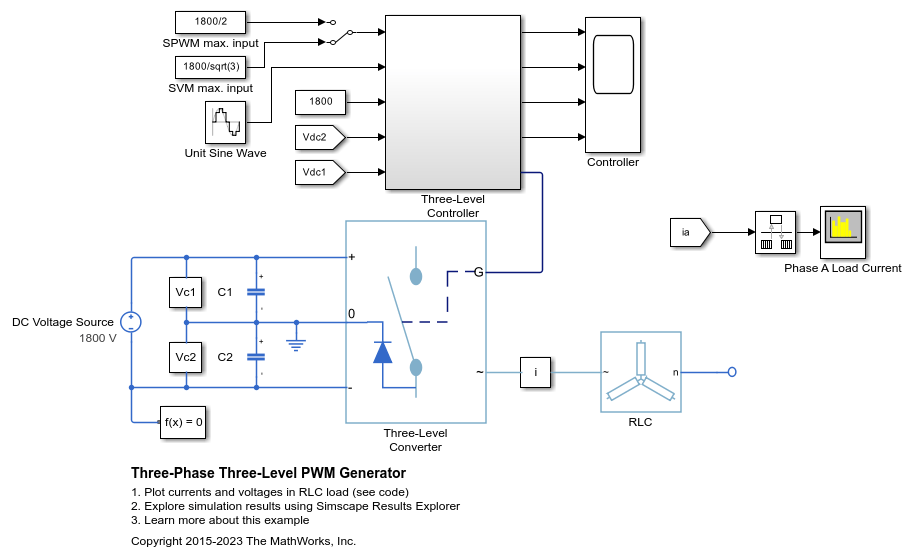
In the Three-Phase Three-Level PWM Generator example, the Three-Level Controller subsystem contains a 1800–V DC-link input, and a modulation index, m, of 0.8. For SVM, the maximal input voltage is V, that is 1039.23 V. To demonstrate overmodulation, a transient is added at the beginning of the simulation. The transient forces the amplitudes of the reference voltages to exceed the amplitude of of the DC-link voltage. To highlight overmodulation, the scope includes simulation results for only one of the 12 output pulses and only the a-phase of the reference voltages, modulation waveforms, and output voltages.

The modulation index is greater than one between 0.03–0.09 seconds. During overmodulation:
The pulse remains in the on or off position.
The output voltage clamps to the positive or negative DC rail.
Examples
Ports
Input
Output
Parameters
References
[1] Chung, D. W., J. S. Kim, and S. K. Sul. “Unified Voltage Modulation Technique for Real Time Three-Phase Power Conversion.” IEEE Transactions on Industry Applications, Vol. 34, No. 2, 1998, pp. 374–380.
[2] Seo, J. H., C. H. Choi, and D. S. Hyun. “A new simplified space-vector PWM method for three-level inverters.” IEEE Transactions on Power Electronics, Vol. 16, No. 4, 2001, pp. 545-550.
Extended Capabilities
Version History
Introduced in R2016b