Three-Winding Transformer (Three-Phase)
Three-phase linear nonideal wye- and delta-configurable three-winding transformer with saturation capability
Libraries:
Simscape /
Electrical /
Passive /
Transformers
Description
The Three-Winding Transformer (Three-Phase) block represents a linear nonideal three-phase three-winding transformer that transfers electrical energy between two or more circuits through electromagnetic induction. The block includes linear winding leakage and linear core magnetization effects. You can parameterize the block impedance using per-unit values. The primary, first secondary , and second secondary winding types, delta-wye phase angle, and core types are configurable.
The configuration options for the primary and secondary winding types are:
Wye with floating neutral — Star or T configuration with Floating Neutral (Three-Phase)
Wye with neutral port — Star or T configuration with Neutral Port (Three-Phase)
Wye with grounded neutral — Star or T configuration with Grounded Neutral (Three-Phase)
Delta 1 o'clock — Mesh configuration with a lagging 30 degree phase shift relative to the voltage of a connected wye configuration
Delta 11 o'clock — Mesh configuration with leading 30 degree phase shift relative to the voltage of a connected wye configuration
Options for the core type are:
Three-phase five-limb
Three-phase three-limb
Although a three-limbs core is typically less expensive, a five-limb core offers these advantages:
Lower impedance for the zero-sequence component of current, that is between the line and neutral, in the case of an unbalanced load
Greater heat dissipation
Equations
This block is implemented in the magnetic domain using basic magnetic reluctances, windings, and eddy currents blocks.
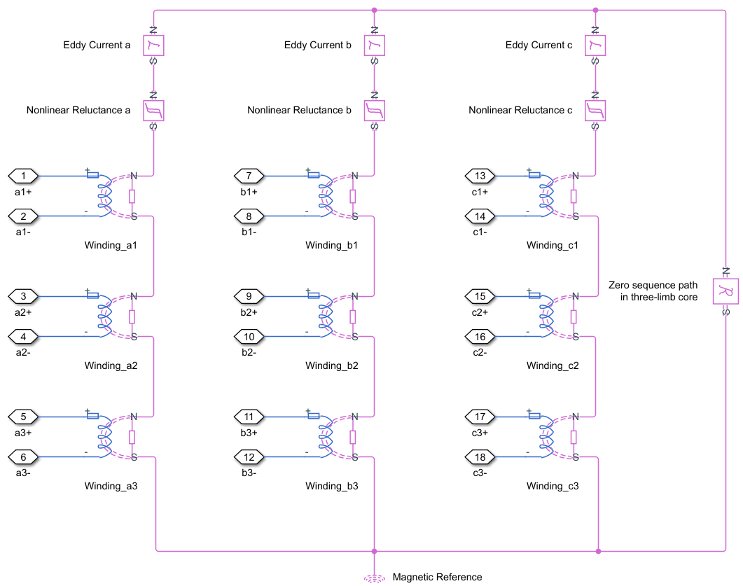
It is important to determine the relation between the electrical domain parameters from the block mask and the magnetic domain parameters used in the model:
n1 is the number of the primary winding turns.
n2 is the number of the first secondary winding turns.
n3 is the number of the second secondary winding turns.
Lm is the shunt magnetizing inductance.
L0 is the zero-sequence inductance.
Lp is the primary winding leakage inductance.
Ls1 is the first secondary winding leakage inductance.
Ls2 is the second secondary winding leakage inductance.
Rm is the shunt magnetizing resistance.
R is the magnetizing reluctance between phases.
R0 is the zero sequence reluctance.
Rl1 is the primary winding leakage reluctance.
Rl2 is the first winding secondary leakage reluctance.
Rl3 is the second winding secondary leakage reluctance.
Leddy is the conductance of eddy current loop
For three-winding transformers (three-phase), the coupling between different windings in each phase is identical.
In the case of a five-limb transformer, the extra magnetic flux paths provided by the extra limbs can be represented by zero sequence reluctances, which are originally designed for magnetic paths through the air in the three-limb transformer.
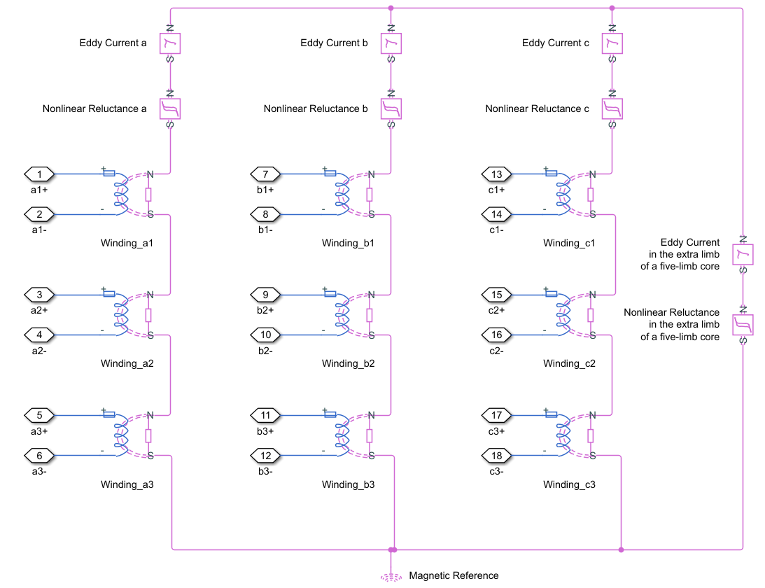
In a five-limb model, the magnetic reluctances from the phases to the extra limbs are supposed to be equal to the magnetic reluctances between phases.
Therefore we deduce:
Display Options
You can display the transformer per-unit base values in the MATLAB® command window using the block context menu. To display the values, right-click the block and select Electrical > Display Base Values.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Examples
Ports
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2019a