DBSCAN
Introduction to DBSCAN
Density-Based Spatial Clustering of Applications with Noise (DBSCAN) identifies
arbitrarily shaped clusters and noise (outliers) in data. The Statistics and Machine Learning Toolbox™ function dbscan
performs clustering on an input data matrix or on pairwise distances between
observations. dbscan returns the cluster indices and a vector
indicating the observations that are core points (points inside clusters). Unlike
k-means clustering, the DBSCAN algorithm does not require
prior knowledge of the number of clusters, and clusters are not necessarily
spheroidal. DBSCAN is also useful for density-based outlier detection, because it
identifies points that do not belong to any cluster.
For a point to be assigned to a cluster, it must satisfy the condition that its
epsilon neighborhood (epsilon) contains at least a minimum number of neighbors (minpts). Or, the point can lie within the epsilon neighborhood of
another point that satisfies the epsilon and
minpts conditions. The DBSCAN algorithm identifies three
kinds of points:
Core point — A point in a cluster that has at least
minptsneighbors in its epsilon neighborhoodBorder point — A point in a cluster that has fewer than
minptsneighbors in its epsilon neighborhoodNoise point — An outlier that does not belong to any cluster
DBSCAN works with a wide range of distance metrics, and you can define a custom distance metric for your particular application. The choice of a distance metric determines the shape of the neighborhood.
Algorithm Description
For specified values of the epsilon neighborhood epsilon
and the minimum number of neighbors minpts
required for a core point, the dbscan
function implements DBSCAN as follows:
From the input data set
X, select the first unlabeled observation x1 as the current point, and initialize the first cluster label C to 1.Find the set of points within the epsilon neighborhood
epsilonof the current point. These points are the neighbors.If the number of neighbors is less than
minpts, then label the current point as a noise point (or an outlier). Go to step 4.Note
dbscancan reassign noise points to clusters if the noise points later satisfy the constraints set byepsilonandminptsfrom some other point inX. This process of reassigning points happens for border points of a cluster.Otherwise, label the current point as a core point belonging to cluster C.
Iterate over each neighbor (new current point) and repeat step 2 until no new neighbors are found that can be labeled as belonging to the current cluster C.
Select the next unlabeled point in
Xas the current point, and increase the cluster count by 1.Repeat steps 2–4 until all points in
Xare labeled.
Determine Values for DBSCAN Parameters
This example shows how to select values for the epsilon and minpts parameters of dbscan. The data set is a Lidar scan, stored as a collection of 3-D points, that contains the coordinates of objects surrounding a vehicle.
Load, preprocess, and visualize the data set.
Load the x, y, z coordinates of the objects.
load('lidar_subset.mat')
X = lidar_subset;To highlight the environment around the vehicle, set the region of interest to span 20 meters to the left and right of the vehicle, 20 meters in front and back of the vehicle, and the area above the surface of the road.
xBound = 20; % in meters yBound = 20; % in meters zLowerBound = 0; % in meters
Crop the data to contain only points within the specified region.
indices = X(:,1) <= xBound & X(:,1) >= -xBound ... & X(:,2) <= yBound & X(:,2) >= -yBound ... & X(:,3) > zLowerBound; X = X(indices,:);
Visualize the data as a 2-D scatter plot. Annotate the plot to highlight the vehicle.
scatter(X(:,1),X(:,2),'.'); annotation('ellipse',[0.48 0.48 .1 .1],'Color','red')
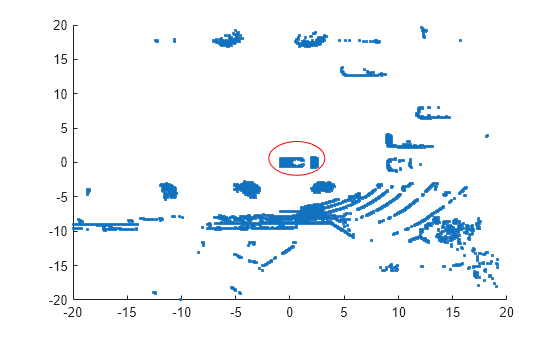
The center of the set of points (circled in red) contains the roof and hood of the vehicle. All other points are obstacles.
Select a value for minpts.
To select a value for minpts, consider a value greater than or equal to one plus the number of dimensions of the input data [1]. For example, for an n-by-p matrix X, set the value of 'minpts' greater than or equal to p+1.
For the given data set, specify a minpts value greater than or equal to 4, specifically the value 50.
minpts = 50; % Minimum number of neighbors for a core pointSelect a value for epsilon.
One strategy for estimating a value for epsilon is to generate a k-distance graph for the input data X. For each point in X, find the distance to the kth nearest point, and plot sorted points against this distance. The graph contains a knee. The distance that corresponds to the knee is generally a good choice for epsilon, because it is the region where points start tailing off into outlier (noise) territory [1].
Before plotting the k-distance graph, first find the minpts smallest pairwise distances for observations in X, in ascending order.
kD = pdist2(X,X,'euc','Smallest',minpts);
Plot the k-distance graph.
plot(sort(kD(end,:))); title('k-distance graph') xlabel('Points sorted with 50th nearest distances') ylabel('50th nearest distances') grid

The knee appears to be around 2; therefore, set the value of epsilon to 2.
epsilon = 2;
Cluster using dbscan.
Use dbscan with the values of minpts and epsilon that were determined in the previous steps.
labels = dbscan(X,epsilon,minpts);
Visualize the clustering and annotate the figure to highlight specific clusters.
numGroups = length(unique(labels)); gscatter(X(:,1),X(:,2),labels,hsv(numGroups)); title('epsilon = 2 and minpts = 50') grid annotation('ellipse',[0.54 0.41 .07 .07],'Color','red') annotation('ellipse',[0.53 0.85 .07 .07],'Color','blue') annotation('ellipse',[0.39 0.85 .07 .07],'Color','black')

dbscan identifies 11 clusters and a set of noise points. The algorithm also identifies the vehicle at the center of the set of points as a distinct cluster.
dbscan identifies some distinct clusters, such as the cluster circled in black (and centered around (–6,18)) and the cluster circled in blue (and centered around (2.5,18)). The function also assigns the group of points circled in red (and centered around (3,–4)) to the same cluster (group 7) as the group of points in the southeast quadrant of the plot. The expectation is that these groups should be in separate clusters.
Use a smaller value for epsilon to split up large clusters and further partition the points.
epsilon2 = 1; labels2 = dbscan(X,epsilon2,minpts);
Visualize the clustering and annotate the figure to highlight specific clusters.
numGroups2 = length(unique(labels2)); gscatter(X(:,1),X(:,2),labels2,hsv(numGroups2)); title('epsilon = 1 and minpts = 50') grid annotation('ellipse',[0.54 0.41 .07 .07],'Color','red') annotation('ellipse',[0.53 0.85 .07 .07],'Color','blue') annotation('ellipse',[0.39 0.85 .07 .07],'Color','black')

By using a smaller epsilon value, dbscan is able to assign the group of points circled in red to a distinct cluster (group 13). However, some clusters that dbscan correctly identified before are now split between cluster points and outliers. For example, see cluster group 2 (circled in black) and cluster group 3 (circled in blue). The correct epsilon value is somewhere between 1 and 2.
Use an epsilon value of 1.55 to cluster the data.
epsilon3 = 1.55; labels3 = dbscan(X,epsilon3,minpts);
Visualize the clustering and annotate the figure to highlight specific clusters.
numGroups3 = length(unique(labels3)); gscatter(X(:,1),X(:,2),labels3,hsv(numGroups3)); title('epsilon = 1.55 and minpts = 50') grid annotation('ellipse',[0.54 0.41 .07 .07],'Color','red') annotation('ellipse',[0.53 0.85 .07 .07],'Color','blue') annotation('ellipse',[0.39 0.85 .07 .07],'Color','black')

dbscan does a better job of identifying the clusters when epsilon is set to 1.55. For example, the function identifies the distinct clusters circled in red, black, and blue (with centers around (3,–4), (–6,18), and (2.5,18), respectively).
References
[1] Ester, M., H.-P. Kriegel, J. Sander, and X. Xiaowei. “A density-based algorithm for discovering clusters in large spatial databases with noise.” In Proceedings of the Second International Conference on Knowledge Discovery in Databases and Data Mining, 226-231. Portland, OR: AAAI Press, 1996.