Recognize and Avoid Round-Off Errors
When approximating a value numerically, remember that floating-point results can be sensitive to the precision used. Also, floating-point results are prone to round-off errors. The following approaches can help you recognize and avoid incorrect results.
Use Symbolic Computations When Possible
Performing computations symbolically is recommended because exact symbolic computations are not prone to round-off errors. For example, standard mathematical constants have their own symbolic representations in Symbolic Math Toolbox™:
pi sym(pi)
ans =
3.1416
ans =
piAvoid unnecessary use of numeric approximations. A floating-point
number approximates a constant; it is not the constant itself. Using
this approximation, you can get incorrect results. For example, the heaviside special
function returns different results for the sine of sym(pi) and
the sine of the numeric approximation of pi:
heaviside(sin(sym(pi))) heaviside(sin(pi))
ans =
1/2
ans =
1Perform Calculations with Increased Precision
The Riemann hypothesis states that all nontrivial zeros of the Riemann Zeta function ζ(z) have the same real part ℜ(z) = 1/2. To locate possible zeros of the Zeta function, plot its absolute value |ζ(1/2 + iy)|. The following plot shows the first three nontrivial roots of the Zeta function |ζ(1/2 + iy)|.
syms y
fplot(abs(zeta(1/2 + i*y)), [0 30])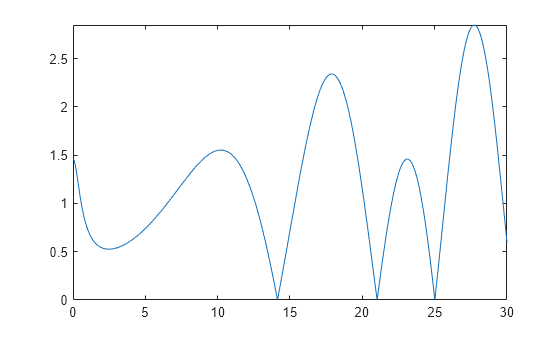
Use the numeric solver vpasolve to
approximate the first three zeros of this Zeta function:
vpasolve(zeta(1/2 + i*y), y, 15) vpasolve(zeta(1/2 + i*y), y, 20) vpasolve(zeta(1/2 + i*y), y, 25)
ans = 14.134725141734693790457251983562 ans = 21.022039638771554992628479593897 ans = 25.010857580145688763213790992563
Now, consider the same function, but slightly increase the real
part, . According to the Riemann hypothesis,
this function does not have a zero for any real value y.
If you use vpasolve with the 10 significant decimal
digits, the solver finds the following (nonexisting) zero of the Zeta
function:
old = digits; digits(10) vpasolve(zeta(1000000001/2000000000 + i*y), y, 15)
ans = 14.13472514
Increasing the number of digits shows that the result is incorrect. The Zeta function does not have a zero for any real value 14 < y < 15:
digits(15) vpasolve(zeta(1000000001/2000000000 + i*y), y, 15) digits(old)
ans = 14.1347251417347 + 0.000000000499989207306345i
For further computations, restore the default number of digits:
digits(old)
Compare Symbolic and Numeric Results
Bessel functions with half-integer indices return exact symbolic expressions. Approximating these expressions by floating-point numbers can produce very unstable results. For example, the exact symbolic expression for the following Bessel function is:
B = besselj(53/2, sym(pi))
B = (351*2^(1/2)*(119409675/pi^4 - 20300/pi^2 - 315241542000/pi^6... + 445475704038750/pi^8 - 366812794263762000/pi^10 +... 182947881139051297500/pi^12 - 55720697512636766610000/pi^14... + 10174148683695239020903125/pi^16 - 1060253389142977540073062500/pi^18... + 57306695683177936040949028125/pi^20 - 1331871030107060331702688875000/pi^22... + 8490677816932509614604641578125/pi^24 + 1))/pi^2
Use vpa to approximate this expression
with the 10-digit accuracy:
vpa(B, 10)
ans = -2854.225191
Now, call the Bessel function with the floating-point parameter. Significant difference between these two approximations indicates that one or both results are incorrect:
besselj(53/2, pi)
ans = 6.9001e-23
Increase the numeric working precision to obtain a more accurate
approximation for B:
vpa(B, 50)
ans = 0.000000000000000000000069001456069172842068862232841396473796597233761161
Plot the Function or Expression
Plotting the results can help you recognize incorrect approximations. For example, the numeric approximation of the following Bessel function returns:
B = besselj(53/2, sym(pi)); vpa(B, 10)
ans = -2854.225191
Plot this Bessel function for the values of x around 53/2.
The function plot shows that the approximation is incorrect:
syms x
fplot(besselj(x, sym(pi)), [26 27])