Validate Simulink Model Using Symbolic Math Toolbox
This example shows how to model a bouncing ball, which is a classical hybrid dynamic system. This model includes both continuous dynamics and discrete transitions. It uses the Symbolic Math Toolbox™ to help explain some of the theory behind ODE solving in the Simulation of Bouncing Ball (Simulink).
Assumptions
The ball rebounds with no angle
There is no drag
Height at time t=0 is 10 m
Thrown with upwards velocity of 15 m/s
Derivation
The coefficient of restitution is defined as
where v is the speed of object before impact and u is the speed after.

We split the second order differential equation
into
discretized as
and
discretized as
We will use basic 1st order numerical integration using forward Euler.
Solve the Problem Analytically
Using the Symbolic Math Toolbox, we can approach the problem analytically. This allows us to solve certain problems more easily, such as determining precisely when the ball first hits the ground (below).
Declare our symbolic variables.
syms g t H(t) h_0 v_0
Split the second order differential equation into and .
Dh = diff(H); D2h = diff(H, 2) == g
D2h(t) =
Solve the ODE using dsolve:
eqn = dsolve(D2h, H(0) == h_0, Dh(0) == v_0)
eqn =
Parametrically explore the parabolic profile of motion using subs:
eqn = subs(eqn, [h_0, v_0, g], [10, 15, -9.81])
eqn =
Find the time at which the ball hits the ground by solving for zero:
assume(t > 0) tHit = solve(eqn == 0)
tHit =
Visualize the solution:
fplot(eqn,[0 10]) ylim([0 25])

Format your exact results using variable precision arithmetic with vpa:
disp(['The ball with an initial height of 10m and velocity of 15m/s will hit the ground at ' char(vpa(tHit, 4)) ' seconds.'])
The ball with an initial height of 10m and velocity of 15m/s will hit the ground at 3.621 seconds.
Solve the Problem Numerically
Setup Simulation Parameters
Properties of the ball
c_bounce = .9; % Bouncing's coefficient of restitution; perfect restitution would be 1Properties of the simulation
gravity = 9.8; % Gravity's acceleration (m/s) height_0 = 10; % Initial height at time t=0 (m) velocity_0=15; % Initial velocity at time t=0 (m/s)
Declaring the simulation time step
dt = 0.05; % Animation timestep (s) t_final = 25; % Simulate period (s) t = 0:dt:t_final; % Timespan N = length(t); % Number of iterations
Initialize simulation quantities
h=[]; % Height of the ball as a function of time (m) v=[]; % Velocity of the ball (m/sec) as a function of time (m/s) h(1)=height_0; v(1)=velocity_0;
Simulate the bouncing ball (we will use basic 1st order numerical integration using forward Euler):
for i=1:N-1 v(i+1)=v(i)-gravity*dt; h(i+1)=h(i)+v(i)*dt; % When the ball bounces (the height is less than 0), % reverse the velocity and recalculate the position. % Using the coefficient of restitution if h(i+1) < 0 v(i)=-v(i)*c_bounce; v(i+1)=v(i)-gravity*dt; h(i+1)=0+v(i)*dt; end end
Visualize and validate the simulation
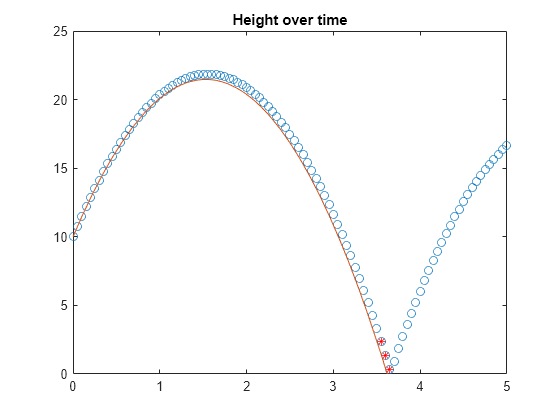
plot(t,h,'o') hold on fplot(eqn,[0 10]) title('Height over time') ylim([0 25]) hold off

plot(t,v)
title('Velocity over time')
Validate Numerics with Analytics
Compare your analytical results with your numeric results.
As a reminder the time of impact was:
disp(['The ball with an initial height of 10m and velocity of 15m/s will hit the ground at ' char(vpa(tHit, 4)) ' seconds.'])
The ball with an initial height of 10m and velocity of 15m/s will hit the ground at 3.621 seconds.
From the numerical simulation we can find the closest value in the simulation when
i = ceil(double(tHit/dt)); t([i-1 i i+1])
ans = 1×3
3.5500 3.6000 3.6500
plot(t,h,'o') hold on fplot(eqn,[0 10]) plot(t([i-1 i i+1 ]),h([i-1 i i+1 ]),'*R') title('Height over time') xlim([0 5]) ylim([0 25]) hold off