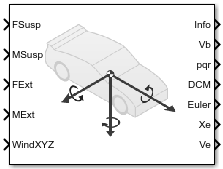
Vehicle Body 6DOF
Two-axle vehicle body with translational and rotational motion
Libraries:
Vehicle Dynamics Blockset /
Vehicle Body
Description
The Vehicle Body 6DOF block implements a six degrees-of-freedom (DOF) rigid two-axle vehicle body model to calculate longitudinal, lateral, vertical, pitch, roll, and yaw motion. The block accounts for body mass, inertia, aerodynamic drag, road incline, and weight distribution between the axles due to suspension and external forces and moments. Use the Inertial Loads parameters to analyze the vehicle dynamics under different loading conditions.
You can connect the block to virtual sensors, suspension system, or external systems like body control actuators. Use the Vehicle Body 6DOF block in ride and handling studies to model the effects of drag forces, passenger loading, and suspension hardpoint locations.
To create additional input ports, under Input signals, select these block parameters.
Parameter | Input Port | Description |
|---|---|---|
| Front hitch forces | FhF | Hitch force applied to the body at the front hitch location, FhFx, FhFy, and FhFz, in the vehicle-fixed frame |
| Front hitch moments | MhF | Hitch moment at the front hitch location, MhFx, MhFy, and MhFz, about the vehicle-fixed frame |
| Rear hitch forces | FhR | Hitch force applied to the body at the rear hitch location, FhRx, FhRy, and FhRz, in the vehicle-fixed frame |
| Rear hitch moments | MhR | Hitch moment at the rear hitch location, MhRx, MhRy, and MhRz, about the vehicle-fixed frame |
Inertial Loads
To analyze the vehicle dynamics under different loading conditions, use the Inertial Loads parameters. Specifically, you can specify these loads:
Front powertrain
Front and rear row passengers
Overhead cargo
Rear cargo
For each of the loads, you can specify the mass, location, and inertia.
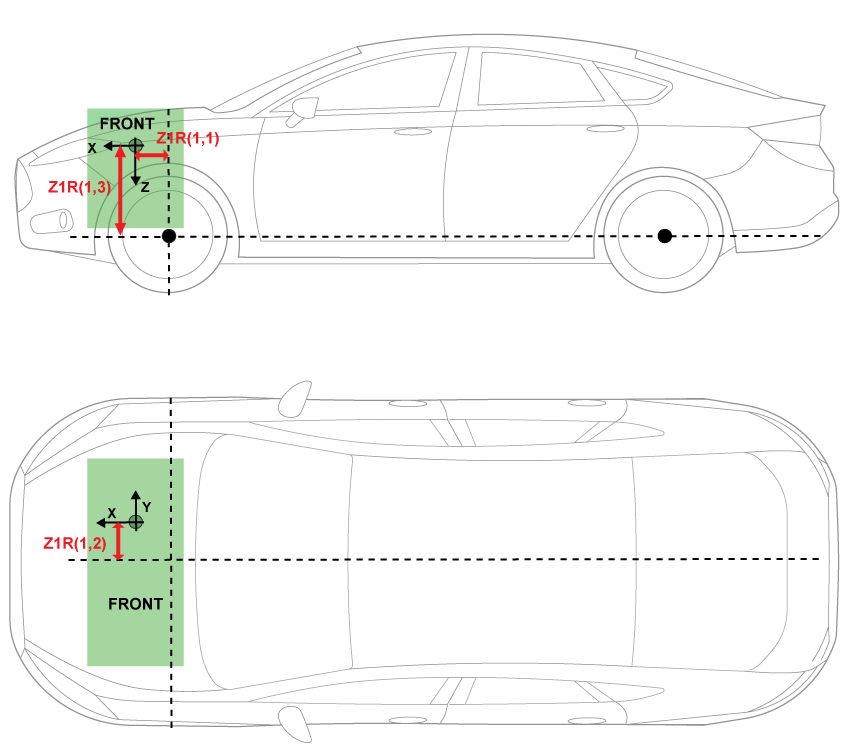
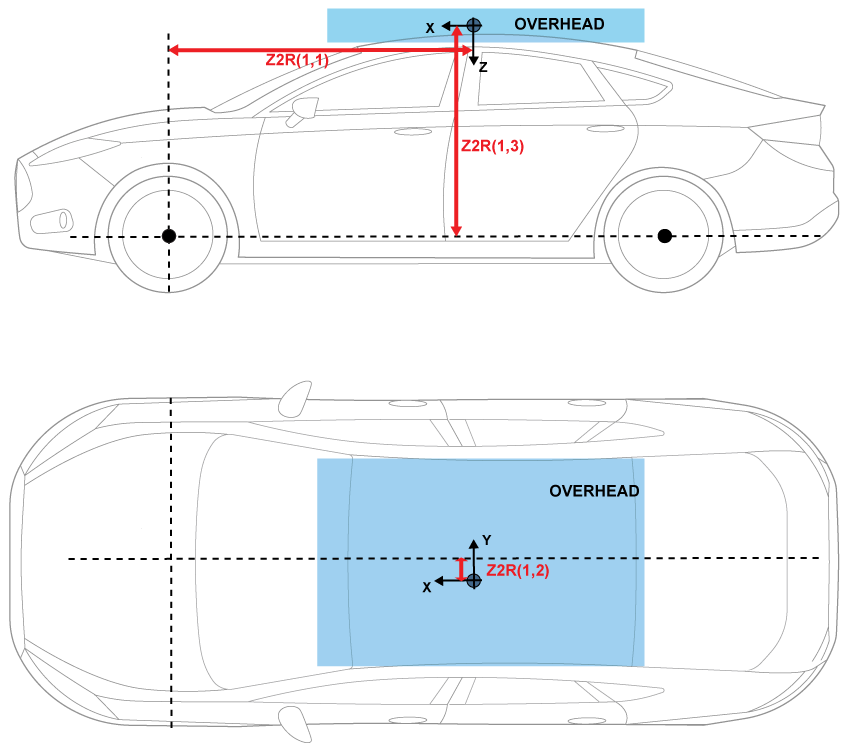
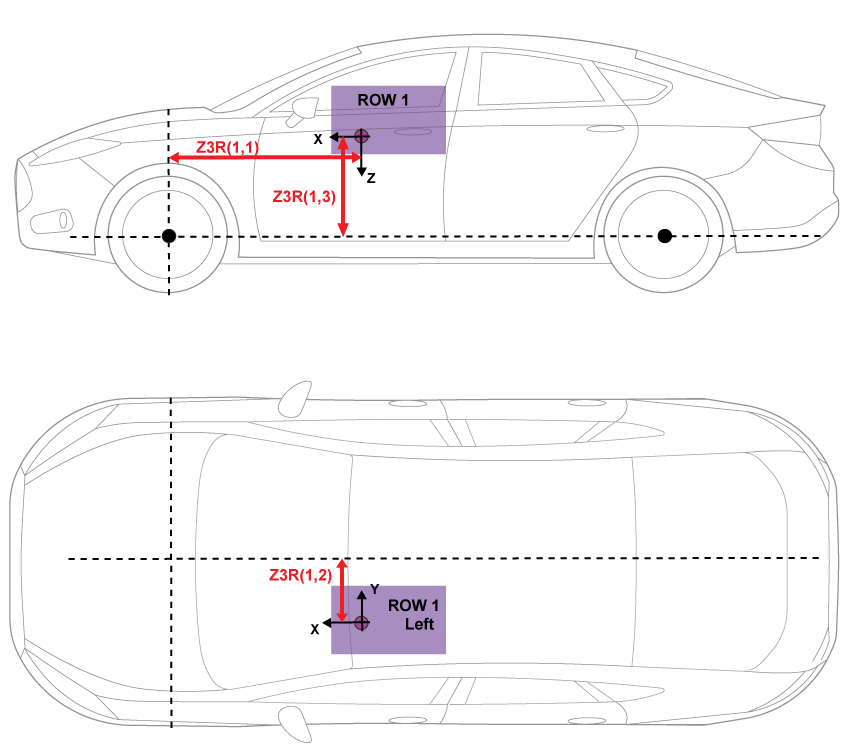
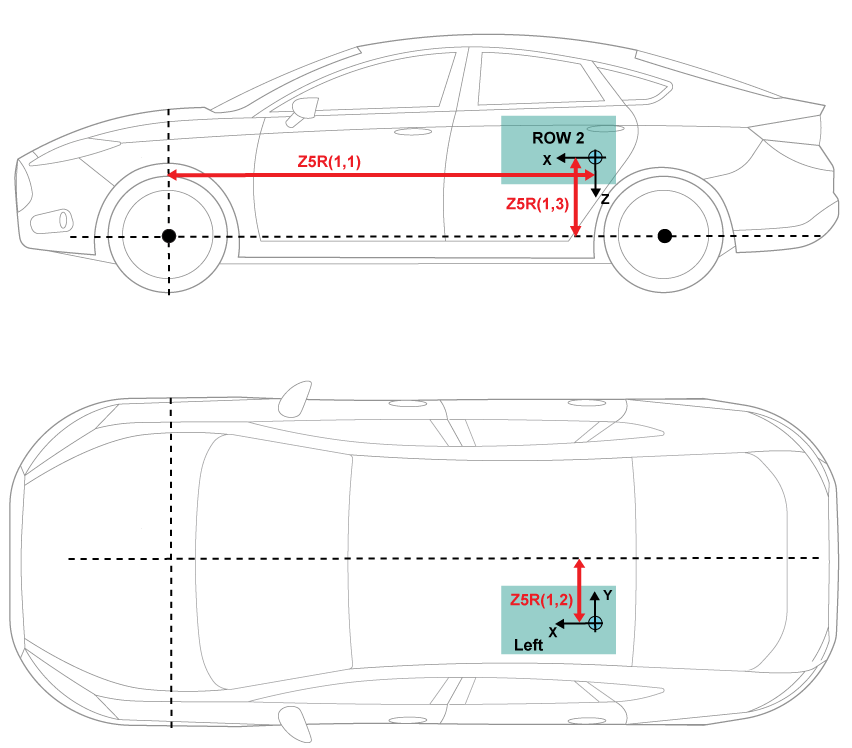
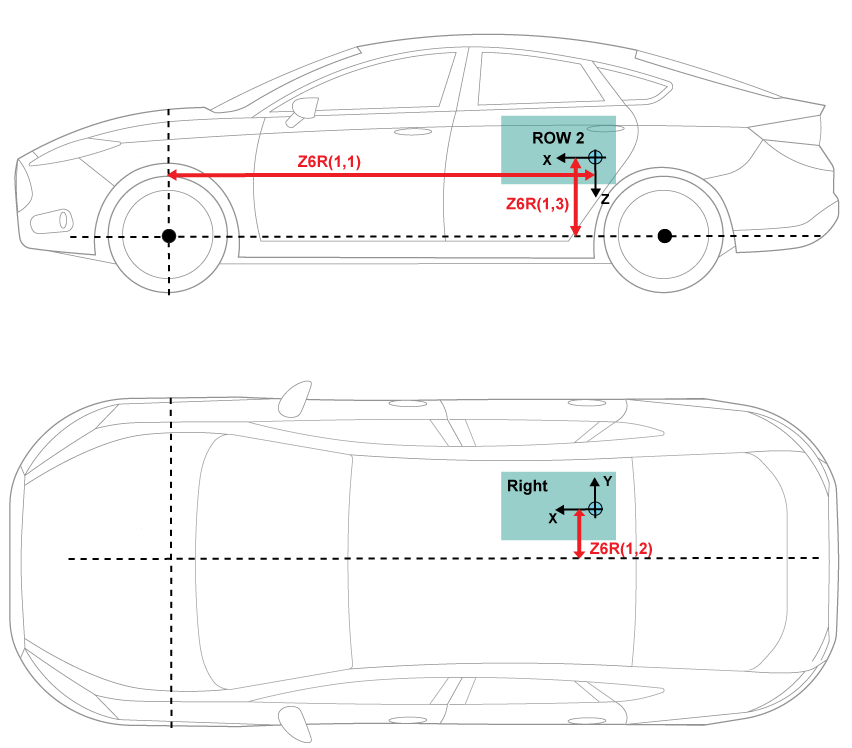
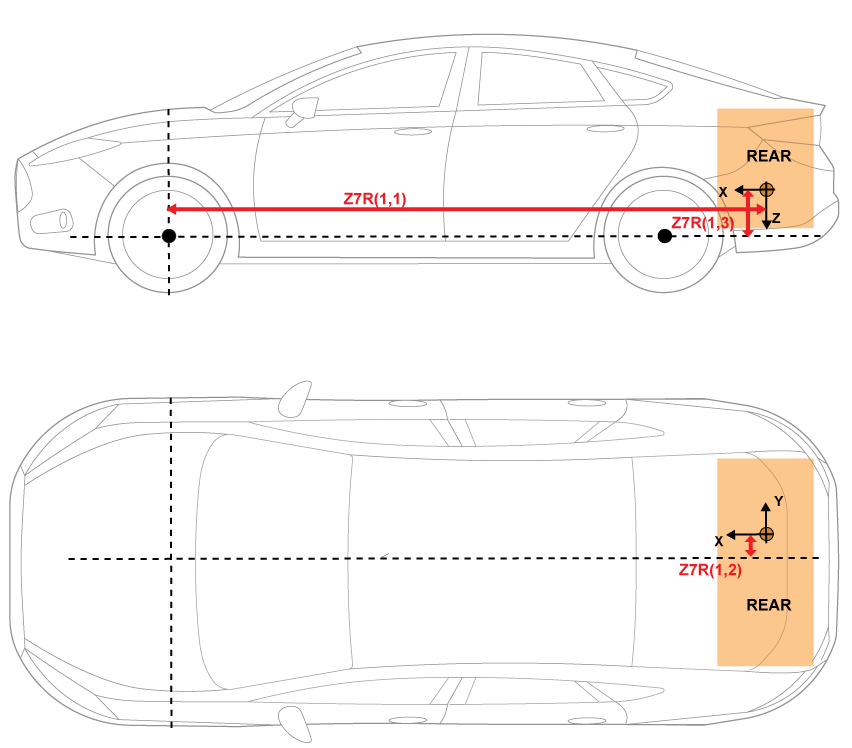
The illustrations provide the load locations and vehicle parameter dimensions. The table provides the corresponding location parameter sign settings.

This table summarizes the parameter settings that specify the load locations indicated by the dots. For the location, the block uses this distance vector:
Front suspension hardpoint to load, along the vehicle-fixed x-axis
Vehicle centerline to load, along the vehicle-fixed y-axis
Front suspension hardpoint to load, along the vehicle-fixed z-axis
Load | Parameter | Example Location |
|---|---|---|
Front | Distance vector from front axle, z1R |
|
Overhead | Distance vector from front axle, z2R |
|
Row 1, left side | Distance vector from front axle, z3R |
|
Row 1, right side | Distance vector from front axle, z4R |
|
Row 2, left side | Distance vector from front axle, z5R |
|
Row 2, right side | Distance vector from front axle, z6R |
|
Rear | Distance vector from front axle, z7R |
|
Equations of Motion
To determine the vehicle motion, the block implements calculations for the rigid body vehicle dynamics, wind drag, inertial loads, and coordinate transformations. The body-fixed and the vehicle-fixed are the same coordinate systems.
The Vehicle Body 6DOF block considers the rotation of a body-fixed coordinate frame about a flat earth-fixed inertial reference frame. The origin of the body-fixed coordinate frame is the vehicle center of gravity of the body.

The block uses this equation to calculate the translational motion of the body-fixed coordinate frame, where the applied forces [Fx Fy Fz]T are in the body-fixed frame, and the mass of the body, m, is assumed constant.
To determine the relationship between the body-fixed angular velocity vector, [p q r]T, and the rate of change of the Euler angles, , the block resolves the Euler rates into the body-fixed frame.
Inverting J gives the required relationship to determine the Euler rate vector.
The applied forces and moments are the sum of the drag, gravitational, external, and suspension forces.
| Calculation | Implementation |
|---|---|
Load masses and inertias | Block uses parallel axis theorem to resolve the individual load masses and inertias with the vehicle mass and inertia. |
Gravitational forces, Fg | Block uses direction cosine matrix (DCM) to transform the gravitational vector in the inertial-fixed frame to the body-fixed frame. |
Drag forces, Fd, and moments, Md | To determine a relative airspeed, the block subtracts the wind speed from the vehicle center of mass (CM) velocity. Using the relative airspeed, the block determines the drag forces. Using the relative airspeed, the block determines the drag moments. |
External forces, Fin, and moments, Min | External forces and moments are input via ports
|
Suspension forces and moments | Block assumes that the suspension forces and moments act on these hardpoint locations:
|
The equations use these variables.
Vehicle CM displacement, velocity, and acceleration along the vehicle-fixed x-axis | |
Vehicle CM displacement, velocity, and acceleration along the vehicle-fixed y-axis | |
Vehicle CM displacement, velocity, and acceleration along the vehicle-fixed z-axis | |
φ | Rotation of the vehicle-fixed frame about the earth-fixed X-axis (roll) |
θ | Rotation of the vehicle-fixed frame about the earth-fixed Y-axis (pitch) |
ψ | Rotation of the vehicle-fixed frame about the earth-fixed Z-axis (yaw) |
| FFLx, FFLy, FFLz | Suspension forces applied to front left hardpoint along the vehicle-fixed x-, y-, and z-axes |
| FFRx, FFRy, FFRz | Suspension forces applied to front right hardpoint along the vehicle-fixed x-, y-, and z-axes |
| FRLx, FRLy, FRLz | Suspension forces applied to rear left hardpoint along the vehicle-fixed x-, y-, and z-axes |
| FRRx, FRRy, FRRz | Suspension forces applied to rear right hardpoint along the vehicle-fixed x-, y-, and z-axes |
| MFx, FFy, FFz | Suspension moments applied to vehicle CM about the vehicle-fixed x-, y-, and z-axes |
| Fextx, Fexty, Fextz | External forces applied to vehicle CM along the vehicle-fixed x-, y-, and z-axes |
| Fdx, Fdy, Fdz | Drag forces applied to vehicle CM along the vehicle-fixed x-, y-, and z-axes |
| Mextx, Mexty, Mextz | External moment about vehicle CM about the vehicle-fixed x-, y-, and z-axes |
| Mdx, Mdy, Mdz | Drag moment about vehicle CM about the vehicle-fixed x-, y-, and z-axes |
| I | Vehicle body moments of inertia |
| a, b | Distance of front and rear wheels, respectively, from the normal projection point of vehicle CM onto the common axle plane |
| d | Lateral distance from the geometric centerline to the center of mass along the vehicle-fixed y-axis |
| h | Height of vehicle CM above the axle plane |
| hh | Height of the hitch above the axle plane along the vehicle-fixed z-axis |
| dh | Longitudinal distance of the hitch from the normal projection point of tractor CG onto the common axle plane |
| hl | Lateral distance from center of mass to hitch along the vehicle-fixed y-axis. |
| wF, wR | Front and rear track widths |
| Cd | Air drag coefficient acting along the vehicle-fixed x-axis |
| Cs | Air drag coefficient acting along the vehicle-fixed y-axis |
| Cl | Air drag coefficient acting along the vehicle-fixed z-axis |
| Crm | Air drag roll moment acting about vehicle-fixed x-axis |
| Cpm | Air drag pitch moment acting about the vehicle-fixed y-axis |
| Cym | Air drag yaw moment acting about vehicle-fixed z-axis |
| Af | Frontal area |
| R | Atmospheric specific gas constant |
| T | Environmental air temperature |
| Pabs | Environmental absolute pressure |
| wx, wy, wz | Wind speed along the vehicle-fixed x-, y-, and z-axes |
| Wx, Wy, Wz | Wind speed along inertial X-, Y-, and Z-axes |
Examples
Ports
Input
Output
Parameters
References
[1] Gillespie, Thomas. Fundamentals of Vehicle Dynamics. Warrendale, PA: Society of Automotive Engineers (SAE), 1992.
Extended Capabilities
Version History
Introduced in R2018a
See Also
6DOF (Euler Angles) (Aerospace Blockset) | Vehicle Body 3DOF | Vector Concatenate