scal2frq

Scale to frequency

Syntax

frq = scal2frq(A,wname,delta)

frq = scal2frq(A,wname)

Description

frq = scal2frq(A,wname,delta) returns the pseudo-frequencies corresponding to the scales given by A and the wavelet specified by wname and the sampling period delta. The output frq is real-valued and has the same dimensions as A.

frq = scal2frq(A,wname) is equivalent to frq = scal2frq(A,wname,1).

Examples

collapse all

Scales and Pseudo-Frequencies

Open Live Script

This example shows how the pseudo-frequency changes as you double the scale.

Construct a vector of scales with 10 voices per octave over five octaves.

vpo = 10;
no = 5;
a0 = 2^(1/vpo);
ind = 0:vpo*no;
sc = a0.^ind;

Verify that the range of scales covers five octaves.

log2(max(sc)/min(sc))

ans = 5.0000

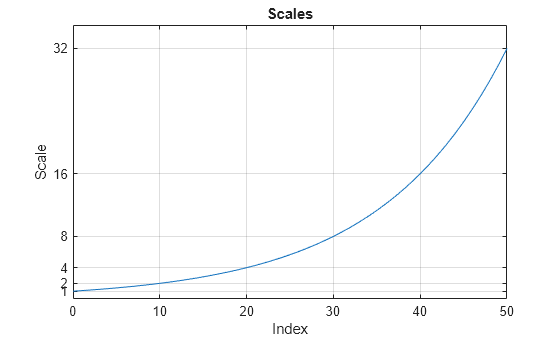
If you plot the scales, you can use a data cursor to confirm that the scale at index $n + 10$ is twice the scale at index $n$ . Set the y-ticks to mark each octave.

plot(ind,sc)
title('Scales')
xlabel('Index')
ylabel('Scale')
grid on
set(gca,'YTick',2.^(0:5))

Figure contains an axes. The axes with title Scales contains an object of type line.

Convert the scales to pseudo-frequencies for the real-valued Morlet wavelet. First, assume the sampling period is 1.

pf = scal2frq(sc,"morl");
T = [sc(:) pf(:)];
T = array2table(T,'VariableNames',{'Scale','Pseudo-Frequency'});
disp(T)

    Scale     Pseudo-Frequency
    ______    ________________

         1          0.8125    
    1.0718         0.75809    
    1.1487         0.70732    
    1.2311         0.65996    
    1.3195         0.61576    
    1.4142         0.57452    
    1.5157         0.53605    
    1.6245         0.50015    
    1.7411         0.46666    
    1.8661         0.43541    
         2         0.40625    
    2.1435         0.37904    
    2.2974         0.35366    
    2.4623         0.32998    
     2.639         0.30788    
    2.8284         0.28726    
    3.0314         0.26803    
     3.249         0.25008    
    3.4822         0.23333    
    3.7321          0.2177    
         4         0.20313    
    4.2871         0.18952    
    4.5948         0.17683    
    4.9246         0.16499    
     5.278         0.15394    
    5.6569         0.14363    
    6.0629         0.13401    
     6.498         0.12504    
    6.9644         0.11666    
    7.4643         0.10885    
         8         0.10156    
    8.5742        0.094761    
    9.1896        0.088415    
    9.8492        0.082494    
    10.556         0.07697    
    11.314        0.071816    
    12.126        0.067006    
    12.996        0.062519    
    13.929        0.058332    
    14.929        0.054426    
        16        0.050781    
    17.148        0.047381    
    18.379        0.044208    
    19.698        0.041247    
    21.112        0.038485    
    22.627        0.035908    
    24.251        0.033503    
    25.992         0.03126    
    27.858        0.029166    
    29.857        0.027213    
        32        0.025391

Assume that data is sampled at 100 Hz. Construct a table with the scales, the corresponding pseudo-frequencies, and periods. Since there are 10 voices per octave, display every tenth row in the table. Observe that for each doubling of the scale, the pseudo-frequency is cut in half.

Fs = 100;
DT = 1/Fs;
pf = scal2frq(sc,"morl",DT);
T = [sc(:)/Fs pf(:) 1./pf(:)];
T = array2table(T,'VariableNames',{'Scale','Pseudo-Frequency','Period'});
T(1:vpo:end,:)

ans=6×3 table
    Scale    Pseudo-Frequency     Period 
    _____    ________________    ________

    0.01           81.25         0.012308
    0.02          40.625         0.024615
    0.04          20.313         0.049231
    0.08          10.156         0.098462
    0.16          5.0781          0.19692
    0.32          2.5391          0.39385

Note the presence of the $Δ t = \frac{1}{F s}$ factor in scal2frq. This is necessary in order to achieve the proper scale-to-frequency conversion. The $Δ t$ is needed to adjust the raw scales properly. For example, with:

f = scal2frq(1,'morl',0.01);

You are really asking what happens to the center frequency of the mother Morlet wavelet, if you dilate the wavelet by 0.01. In other words, what is the effect on the center frequency if instead of $ψ (t)$ , you look at $ψ (t / 0.01)$ . The $Δ t$ provides the correct adjustment factor on the scales.

You could have obtained the same results by first converting the scales to their adjusted sizes and then using scal2frq without specifying $Δ t$ .

scadjusted = sc.*0.01;
pf2 = scal2frq(scadjusted,'morl');
max(pf-pf2)

ans = 0

Plot CWT with Frequencies in a Contour Plot

Open Live Script

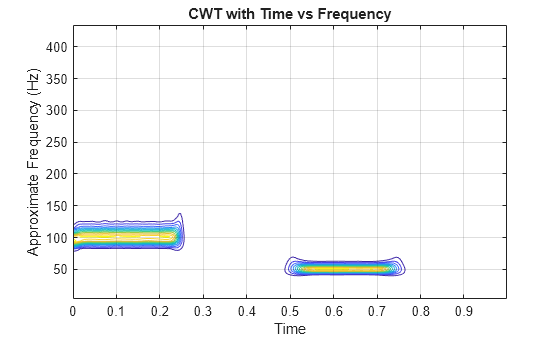
The example shows how to create a contour plot of the CWT using approximate frequencies in Hz.

Create a signal consisting of two sine waves with disjoint support in additive noise. Assume the signal is sampled at 1 kHz.

Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x = 1.5*cos(2*pi*100*t).*(t<0.25)+1.5*cos(2*pi*50*t).*(t>0.5 & t<=0.75);
x = x+0.05*randn(size(t));

Obtain the CWT of the input signal and plot the result.

[cfs,f] = cwt(x,Fs);
contour(t,f,abs(cfs).^2); 
axis tight;
grid on;
xlabel('Time');
ylabel('Approximate Frequency (Hz)');
title('CWT with Time vs Frequency');

Figure contains an axes. The axes with title CWT with Time vs Frequency contains an object of type contour.

Input Arguments

collapse all

`A` — Scales
positive real-valued vector

Scales, specified as a positive real-valued vector.

`wname` — Wavelet
character vector | string scalar

Wavelet, specified as a character vector or string scalar. See wavefun for more information.

`delta` — Sampling period
`1` (default) | positive real-valued scalar

Sampling period, specified as a real-valued scalar.

Example: pf = scal2frq([1:5],"db4",0.01)

More About

collapse all

Pseudo-Frequencies

There is only an approximate answer for the relationship between scale and frequency.

In wavelet analysis, the way to relate scale to frequency is to determine the center frequency of the wavelet, F_c, and use the following relationship:

$F_{a} = \frac{F_{c}}{a}$

where

a is a scale.
F_c is the center frequency of the wavelet in Hz.
F_a is the pseudo-frequency corresponding to the scale a, in Hz.

The idea is to associate with a given wavelet a purely periodic signal of frequency F_c. The frequency maximizing the Fourier transform of the wavelet modulus is F_c. The centfrq function computes the center frequency for a specified wavelet. From the above relationship, it can be seen that scale is inversely proportional to pseudo-frequency. For example, if the scale increases, the wavelet becomes more spread out, resulting in a lower pseudo-frequency.

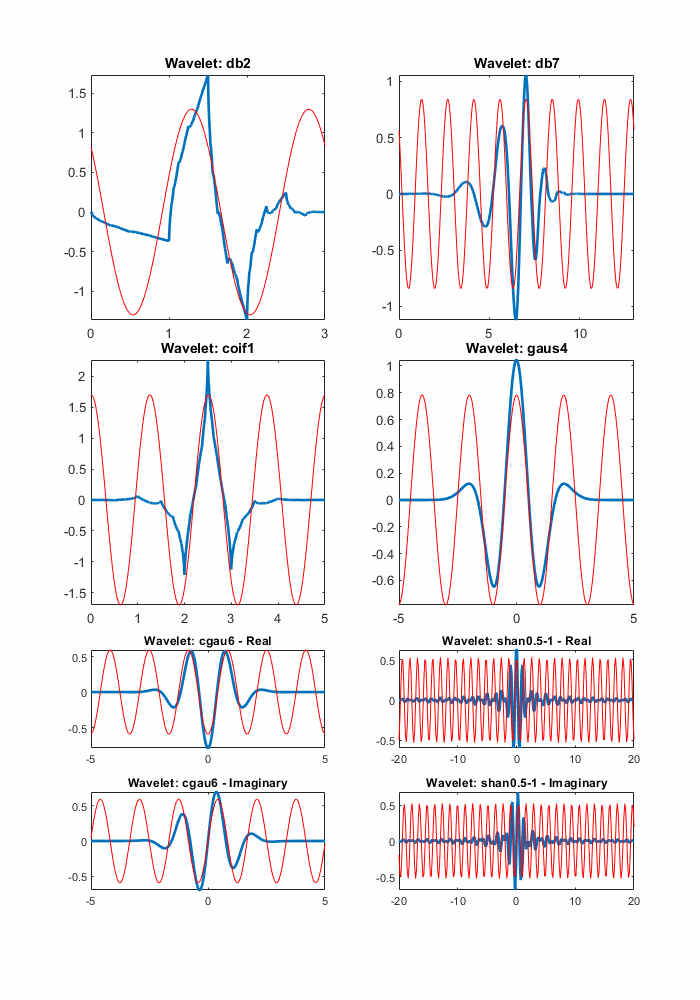
Some examples of the correspondence between the center frequency and the wavelet are shown in the following figure.

Center Frequencies for Real and Complex Wavelets

As you can see, the center frequency-based approximation (red) captures the main wavelet oscillations (blue). The center frequency is a convenient and simple characterization of the dominant frequency of the wavelet.

References

[1] Abry, P. Ondelettes et turbulence. Multirésolutions, algorithmes de décomposition, invariance d'échelles et signaux de pression. Diderot, Editeurs des sciences et des arts, Paris, 1997.