Pebble Game
A MATLAB Toolbox for Two-Dimensional Rigidity Percolation: The Pebble Game
Preface
Welcome to MATLAB toolbox for 2D rigidity percolation. The generical rigidity of graphs plays an essential role in the field of sensor network location. Jacobs et al. provided an exciting and effective method that uses pebble games to percolate the rigidity of a network [2]. To meet the need of research and teaching on MATLAB, we implement the algorithm and build a toolbox. The implementation disassembles the pebble game into elemental actions, which provides interactivity and reusability. Benefitting from the build-in graph operation from MATLAB, the toolbox has good compatibility. The practice shows the following convenience:
-
Analyzing the rigidity of a network with less than ten lines of code.
-
Observing the work of pebble games step by step.
-
Never generating extra variables to contaminate workspace.
-
Generating good figures for papers.
We sincerely hope our toolbox facilitates research and teaching. Any suggestions, corrections, and improvements are welcome.
Please Email: bluebirdhouse@me.com
Concepts
Pebbling is a game that involves placing pebbles on the vertices of a directed acyclic graph according to specific rules [1]. When the pebble game is used to percolate the rigidity of 2D generic networks, the rules are as follows. Each vertex is given two pebbles. The edges are added to the graph one at a time, and pebbles are rearranged to cover the edge. First, we look at the vertices that incident to the newly added edge. If either vertex has a free pebble, then use it to cover the edge. In the meantime, the edge is directed away from the vertex that offers a pebble. If neither of them has free pebbles, their pebbles must have been used to cover existing edges. We should try to free up a pebble for the newly added edge. If a vertex at the other end of existing edges has a free pebble, then that pebble can cover the associated edge. The swap will free up a pebble. More formally, we are searching for a free pebble that follows the directions of edges. This search of a free pebble continues until either a pebble is found and a sequence of swaps allows the new edge to be covered, or else no more vertices can be reached and no free pebbles have been discovered. If we fail to find a free pebble, the new edge will be removed and play no roles in pebble games.
Two tasks should be accomplished when percolating the rigidity of a 2D generic network: identifying independent edges and exploring rigid clusters.
The first task starts from a graph that contains no edge. We randomly add one edge that should be tested to the graph and quadruple the edge; then, four edges are added to the graph one after another to find pebble covering. If four edges are all covered by pebbles, three will be removed from the graph. The left one is an independent edge. If not, we remove all of them and mark the edge redundant.
After every edge is tested, rigid clusters will be explored. Since an independent edge can only belong to one rigid cluster, the triple edge will exhaust three free pebbles of the current rigid cluster. Any vertex that belongs to the same rigid cluster will not collect pebbles from the associated two vertices. The edges between two vertices that fail to find a free pebble are marked as the same rigid cluster.
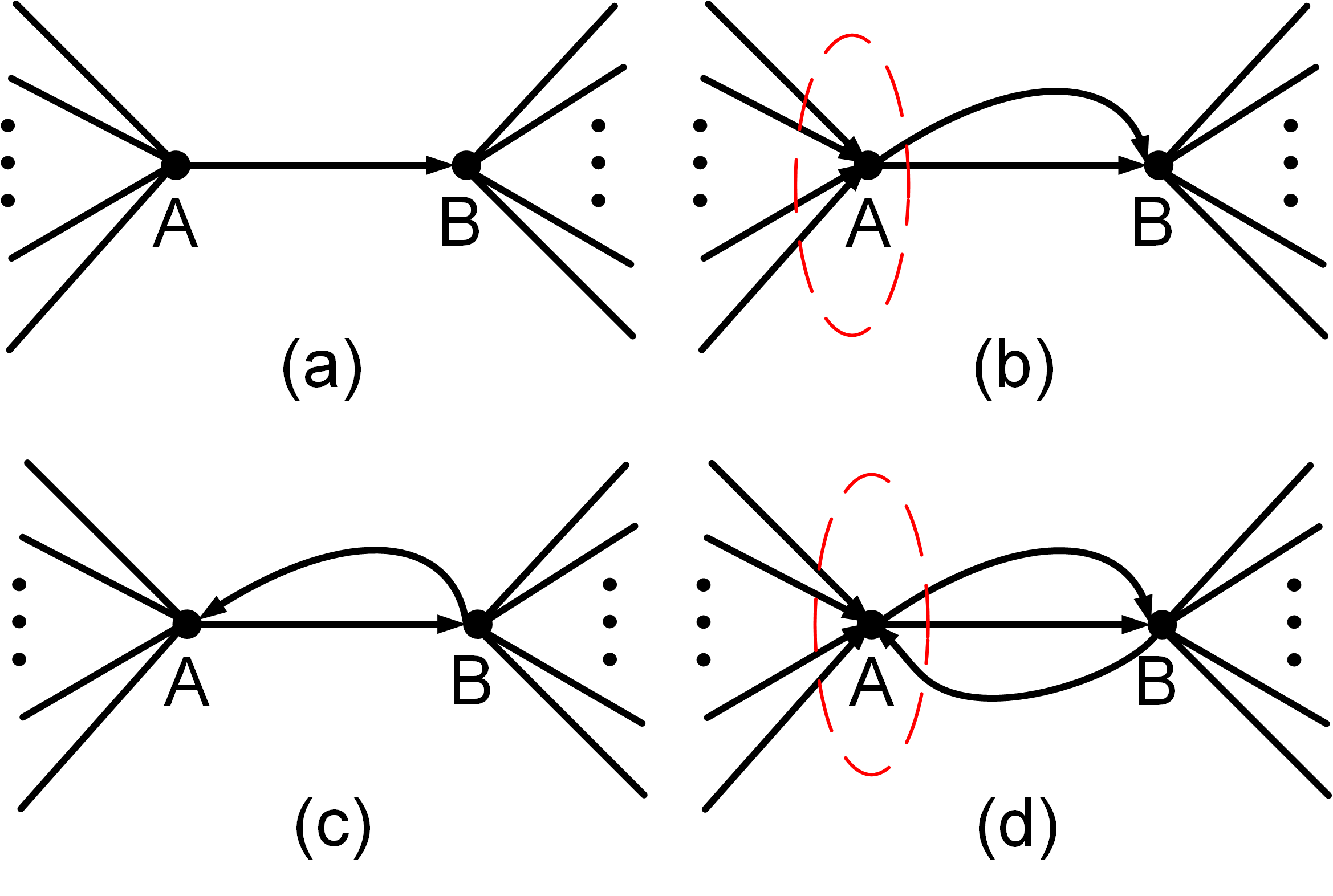
Our toolbox differs from the work [2] in two ways. The toolbox performs a breadth-first search; then, it moves through the search results to find a free pebble. This strategy finds free pebbles faster and is easier to program, but it will consume more memory. Furthermore, we believe that pinning free pebbles at a vertex is equivalent to using free pebbles to cover the edge (Theorem 1). Thus, we pin three pebbles and use the fourth one to cover the edge rather than cover quadruple edges. We will improve this claim.
Theorem 1. Pinning free pebbles at a vertex is equivalent to using free pebbles to cover the edge associated with the vertex.
Figure 1: Testing an independent edge.If a pebble from vertex B covers the double edge, the condition is similar to Figure 1(c). In this condition, freeing a pebble from A to B will lead to the condition of Figure 1(b). However, if the third pebble is collected through other paths, the collection has nothing to do with directed edges between A and B.
Two pebbles from vertex A and one from vertex B have been used to cover tripled edges in the last condition (Figure 1(d)). The fourth pebble can only be collected by vertex B and will not from vertex A. The existed three directed edges between A and B do not affect vertex B collecting pebbles.
Since the directed edges between vertex A and vertex B will not affect collecting more pebbles, we can pin pebbles on the vertices rather than covering the first, double, and triple edges.
Q.E.D.
Examples and How-To
The toolbox is based on the build-in graph operation of MATLAB, so it should be compatible with version 7.6 and later. The user may add toolbox files to MATLAB’s search path with m-file ‘SetPath.’ There are examples in the toolbox to play with; then, users get out to build personal stage of pebble game.
Building the Pebble Game Play Stage
The interface of PebbleGamePlayStage is the same as the function graph,
which is a built-in MATLAB class. The first step is to create a table that
contains a variable EndNodes, such as:
T1 = [1 2; 1 4; 1 6; 2 3; 2 4; 2 5; 2 6; 3 4; 3 6; 4 5; 4 6; 5 6];
T2 = [3 7; 3 9; 3 11; 7 8; 7 9; 7 10; 7 11; 8 9; 8 11; 9 10; 9 11; 10 11];
T3 = [5 12; 5 14; 5 16; 12 13; 12 14; 12 15; 12 16; 13 14; 13 16; 14 15; 14 16; 15 16];
T = [T1;T2;T3];
EdgeTable = table(T,'VariableNames',{'EndNodes'});
The table is used as the parameter to instantiate PebbleGamePlayStage.
PebbleGame = PebbleGamePlayStage(EdgeTable);
Then, store two associated vertices of an edge into different matrices.
s = [1 1 1 2 2 2 2 3 3 4 4 5];
t = [2 4 6 3 4 5 6 4 6 5 6 6];
PebbleGame = PebbleGamePlayStage(s,t);
When the instantiation PebbleGame is created, the class UserInPut_Group
is instantiated automatically. Its handle is copied to PebbleGame.UserInPut.
This class shows the user’s input and provides data for instantiating
Operation_Group. The latter, whose handle is PebbleGame.Operation,
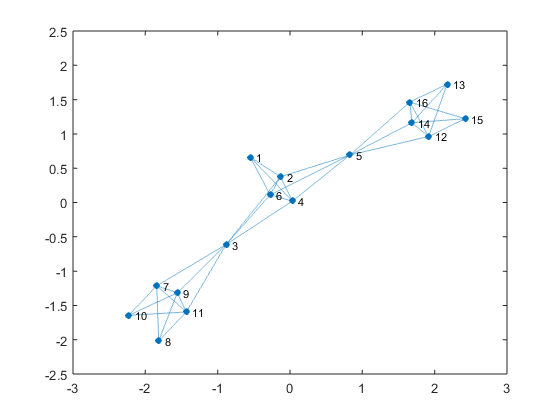
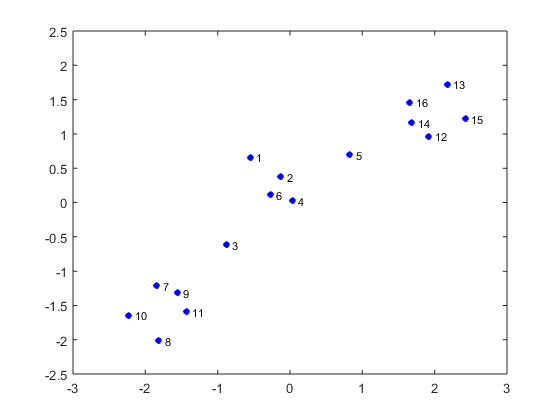
identifies independent edges and explores rigid clusters. The MATLAB will pop up
two figures, such as Figure 2 and Figure 3. One shows the user’s input, the
other displays the process of the pebble game.
Playing Pebble Games
The toolbox contains multiple functions to customize pebble games. However, if the user prefers identifying independent edges with the classic pebble game [2], only one function should be enough.
for i = 1:1:(12*3)
PebbleGame.Operation.IndependentEdge(1)
drawnow();
end
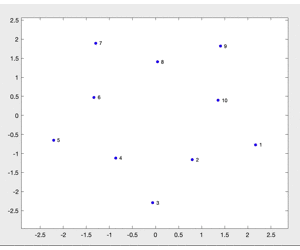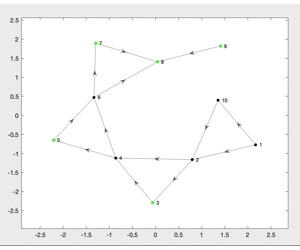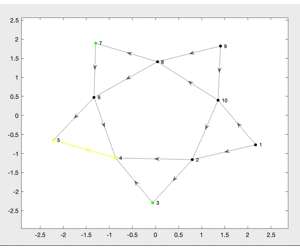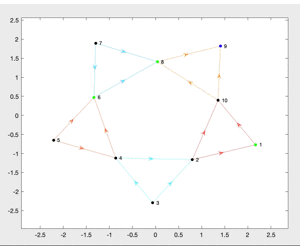
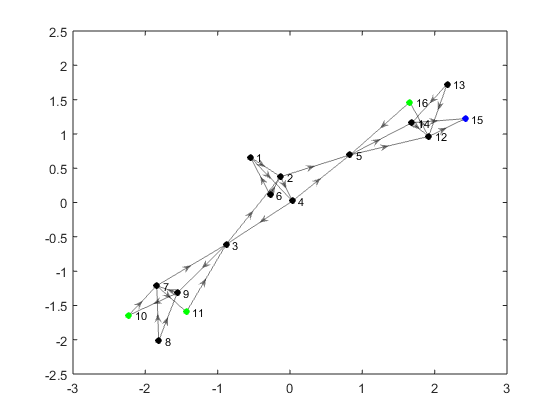
Each time the function IndependentEdge is called, it picks an edge from
PebbleGame.Operation.EdgeReadyForAdd and try to find a free pebble to cover
it. If the edge is independent, the function adds it to the graph; otherwise,
the function adds it to PebbleGame.Operation.EdgeUnableAdd. Eventually, the
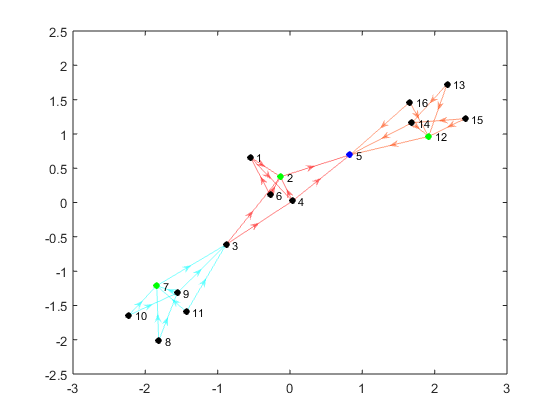
graph will be like Figure 4.
Identifying Rigid Clusters and Coloring Them
Before exploring rigid clusters, the user executes function
StartIdentifyRigidCluster to get the toolbox ready.
PebbleGame.Operation.StartIdentifyRigidCluster();
The code below explores rigid clusters as many as there are.
while(PebbleGame.Operation.IdentifyARigidCluster() == false)
PebbleGame.Operation.ShowRigidCluster();
drawnow();
end
As shown in Figure 5, the function ShowRigidCluster can color the rigid
clusters. Use drawnow wisely to show a dynamic figure.
Acknowledgments
-
The toolbox uses a class
ArrayListfrom an excellent MATLAB-based robot software Sim.I.am [3]. -
The suggestion of professor Jacobs, which is to build an easy-to-use interface, gave us confidence about the work.
-
Professor Hongxia Wang gave attention and encouragement during the software development.
-
Professor Li Yu provided financial support when the software was registered.
-
This work is supported by the Key Programs of the Natural Science Foundation of Zhejiang Province under Grant LZ15F030003.
References
[1] Wikipedia contributors. Pebble game [Internet]. Wikipedia, The Free Encyclopedia; 2015 Jul 27, 10:50 UTC [cited 2016 Jan 25]. Available from: https://en.wikipedia.org/w/index.php?title=Pebble_game&oldid=673286933.
[2] D. J. Jacobs and B. Hendrickson, "An algorithm for two-dimensional rigidity percolation: the pebble game," Journal of Computational Physics, vol. 137, pp. 346-365, 1997.
[3] J. P. d. l. Croix. (2013). Sim.I.am. Available: http://jpdelacroix.com/simiam/
Cite As
Blue Bird (2025). Pebble Game (https://github.com/BlueBirdHouse/PebbleGame/releases/tag/v1.0.9), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxTags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
+color
+containers
Examples
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.9 |