Sparse Matrix Gather Operation
No License
If
S=sparse(I,J,V);
then this function is the "inverse" of sparse, in the sense that
V=gather(S,I,J);
For small matrices, an equivalent (and more efficient) version is
S(sub2ind(size(S),I,J));
This version breaks down for matrices for which prod(size) is bigger than 2^31 or so. For square matrices, this limits the size to about 30,000 by 30,000. For purposes such as finite elements, a 30,000 by 30,000 sparse matrix is actually small. The gather operation is mostly not needed except in the mesh subdivision routine, which needs to be able to look up pairs of vertices in a sparse matrix to recover an edge identifier (so that these edges can be subdivided.)
In this situation, for large meshes, the only way I found of not overflowing the 31 bit integers is to use this implementation of the gather operation.
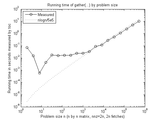
The performance is reasonably good. Because one is reading from a sparse matrix, each access can be expected to take log(n) time (n=size(S,1)). For m accesses, the running time should therefore be mlogn. The associated screenshot is a performance measurement. The running time is measured by
ij=floor(rand(2*n,2)*n+1);
S=sparse(ij(:,1),ij(:,2),round(rand(2*n,1)*n),n,n);
tic;
gather(S,ij(:,1),ij(:,2));
t=toc
The measurement is compared to nlogn/5e5. The two curves are very close, so this algorithm is sound.
Cite As
Sébastien Loisel (2025). Sparse Matrix Gather Operation (https://www.mathworks.com/matlabcentral/fileexchange/13901-sparse-matrix-gather-operation), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Mathematics > Sparse Matrices >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 | Corrected code in description. This includes the changes I made in the previous update. |