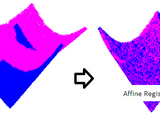
Finite Iterative Closest Point

Iterative Closest Point using finite difference optimization to register 3D point clouds affine.

Description

This function ICP_FINITE is an kind of Iterative Closest Point(ICP) registration algorithm for 3D point clouds (like vertice data of meshes ) using finite difference methods.

Normal ICP solves translation and rotation with analytical equations. By using finite difference this function can also solve resizing and shear thus affine registration.

As first step, this function sorts the static points into a grid of overlapping blocks. The block nearest to a moving point will always contain its closest static point, thus the grid allows faster registration.

• MATLAB release: MATLAB 7.8 (R2009a)

[M.]

Could you please put a reference for this work? Thanks a lot for uploading it.

[yu]

sorry,but i cannot run it successfully. the error is
''??? Error using ==> tic
Too many output arguments......."
btw, my database contains about 40 thousand 3-D points.

expecting your reply.

[Robert]

I tried running this program, and all the points on my data model were transformed to a singular point. If this could be explained, I would revise my rating. For example, put a demo up, so I can see that it works for something you worked with.

[Robert]

Fixed, but a demo code would be a nice addition.

[Jacques Saade]

Hi, really great work! But me too I ask if you can put a reference for the work

[Meidya Koeshardianto]

nice code

[Dirk-Jan Kroon]

* Jacques Saade
The code is written from scratch and not published in a paper.
You can of course reference the original paper.

[JK Hwang]

Hi, Dirk-Jan Kroon. I was wondering about your nearest points searching method in your code. What is the reason why you used a grid spacing term, 'spacing=size(Points_Static,1)^(1/6)*sqrt(3);', in your code when uniform grid of points is established. Is there any reference about that?

[Alex]

This code works perfectly well! Thank you for your nice and really useful work

[Ben]

Can it be used for registering 2D point sets?