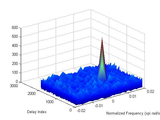
Joint Frequency and Delay Correlation

2D (frequency and delay) circular cross correlation.

Version 1.1.0 (35.2 KB)
2.5K Downloads
(3)
6 Feb 2017
Download

  • Install in MATLAB

    Requires R2026b and later. Learn more
Download

  • Install in MATLAB

    Requires R2026b and later. Learn more

You are now following this Submission

Cite As

Dan Boschen (2026). Joint Frequency and Delay Correlation (https://www.mathworks.com/matlabcentral/fileexchange/26035-joint-frequency-and-delay-correlation), MATLAB Central File Exchange. Retrieved .

Categories

Find more on Correlation and Convolution in Help Center and MATLAB Answers

General Information

MATLAB Release Compatibility

  • Compatible with any release

Platform Compatibility

  • Windows
  • macOS
  • Linux
Open in new tab
Version Published Release Notes
1.1.0

Fixed a typo in the Application Note section describing the fft approach to cross correlation.
Download

  • Install in MATLAB

    Requires R2026b and later. Learn more
1.0.0

Download

  • Install in MATLAB

    Requires R2026b and later. Learn more