Random Numbers from a Discrete Distribution
GENDIST - generate random numbers according to a discrete probability distribution
Tristan Ursell, 2011.
T = gendist(P,N,M)
T = gendist(P,N,M,'plot')
The function gendist(P,N,M) takes in a positive vector P whose values form a discrete probability distribution for the indices of P. The function outputs an N x M matrix of integers corresponding to the indices of P chosen at random from the given underlying distribution.
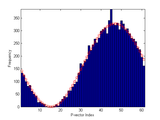
P will be normalized, if it is not normalized already. Both N and M must be greater than or equal to 1. The optional parameter 'plot' creates a plot displaying the input distribution in red and the generated points as a blue histogram.
Conceptual EXAMPLE:
If P = [0.2 0.4 0.4] (note sum(P)=1), then T can only take on values of 1, 2 or 3, corresponding to the possible indices of P. If one calls gendist(P,1,10), then on average the output T should contain two 1's, four 2's and four 3's, in accordance with the values of P, and a possible output might look like:
T = gendist(P,1,10)
T = 2 2 2 3 3 3 1 3 1 3
If, for example, P is a probability distribution for position, with positions X = [5 10 15] (does not have to be linearly spaced), then the set of generated positions is X(T).
EXAMPLE 1:
P = rand(1,50);
T = gendist(P,100,1000,'plot');
EXAMPLE 2:
X = -3:0.1:3;
P = 1+sin(X);
T = gendist(P,100,1000,'plot');
Xrand = X(T);
Cite As
Tristan Ursell (2024). Random Numbers from a Discrete Distribution (https://www.mathworks.com/matlabcentral/fileexchange/34101-random-numbers-from-a-discrete-distribution), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Acknowledgements
Inspired: Random Sample from Discrete PDF
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.