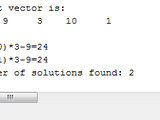
Back in college, I was taught how to play this little math game by a Chinese friend of mine. She told me that they used to play this game quite regularly as kids. As a group of four, we would each plunk down a randomly generated card to have four numbers that may be manipulated in any way using +, *, -, or ÷. For example let's say the cards show 1, 5, 7 and12. One possible solution is 1*(7-5)*12. Recently, I thought it would be fun to write a Matlab program that would find all possible solutions to a group of four numbers. My solution uses a series of nested loops to test for different ordering of the vector in question, different operation combinations, and operation groupings using parentheses. I tried to make the code more efficient by trimming repeated vectors. For example, if the test vector is [10 10 4 4], there are only six unique permutations, instead of the expected 24 (4!). I would love to see if anyone out there can make this code more efficient.
I wanted to test my code to see if it found all possible solutions. For a deck of 13 cards, it turns out that there are nchoosek(16,4) four card combinations, or 1820. From the Wikipedia page, I saw that Cheng Chang published all distinct solutions to the puzzle at http://www.ocf.berkeley.edu/~chechang/24/puzzle_sol.html. Initial versions of the program did not find all solutions. For example it missed the obvious [1 1 2 7], whose solution could simply be (1+2)*(1+7). I added different parentheses combinations hoping to catch more of the solutions. Finally, the algorithm was able to catch all the solutions except for one: [3 3 8 8]. The solution turned out to be tricky: 8/(3-8/3)=24. After eliminating a rounding error, the algorithm now finds all the solutions published on Cheng's page.
Cite As
Raj Sodhi (2024). 24 Game Solver (https://www.mathworks.com/matlabcentral/fileexchange/34368-24-game-solver), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxTags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.