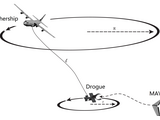
Aerial Recovery Concept Demo (Gauss's Principle)
The towing vehicle (mothership) is commanded to follow a circular orbit that results a circular orbit of the towed body (drogue) with smaller radius and lower velocity relative to the mothership. The miniature aerial vehicle (MAV), which is to be retrieved, is regulated to follow the drogue orbit and to approach the drogue with a relatively low airspeed. After the MAV dock on the drogue, the towed cable and bodies (both drogue and MAV) are reeled into the mothership to complete the aerial recovery.
In this demo, Gauss’s Principle is used to derive the dynamic model of the cable-drogue system. The MAV uses missile guidance strategies to intercept the drogue.
For more information see:
Sun, L., Beard, R. W., and Colton, M. B., McLain, T. W., “Dynamics and Control of Cable-drogue System in Aerial Recovery of Micro Air Vehicles Based on Gauss’s Principle.” St. Louis, MO, USA: American Control Conference, June 2009, pp. 4729–4734.
http://prism.groups.et.byu.net/uploads/Members/SunBeard09.pdf
Colton, M. B., Sun, L., Carlson, D. C., and Beard, R. W., "Multi-vehicle Dynamics and Control for Aerial Recovery of Micro Air Vehicles", Int. J. Vehicle Autonomous Systems, Vol. 9, 2011, pp. 78-107.
http://prism.groups.et.byu.net/uploads/Members/ColtonSun11.pdf
Cite As
Liang Sun (2024). Aerial Recovery Concept Demo (Gauss's Principle) (https://www.mathworks.com/matlabcentral/fileexchange/40561-aerial-recovery-concept-demo-gauss-s-principle), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.