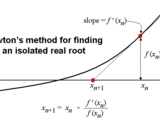
Newton's Method
This function can be used to perform Newton-Raphson method to detect the root of a polynomial. It starts from an initial guess by user and iterates until satisfy the required convergence criterion.
It should be noted that the “root” function in the MATLAB library can find all the roots of a polynomial with arbitrary order. But this method, gives the one the roots based on the initial guess and it gives the number of iteration required to converge.
% Example:
% f(x)=(x^3)-6(X^2)-72(x)-27=0
% therefore
% vector=[1 -6 -72 -27]
% initial=300;
% tolerance=10^-2;
% maxiteration=10^4;
% [root,number_of_iteration] = newton(vector,initial,tolerance,maxiteration)
% or
% [root,number_of_iteration] = newton([1 -6 -72 -27],300,10^-2,10^4)
% root=
% 12.1229
% number_of_iteration=
% 13
% This means that the detected root based on the initial
% guess (300) is 12.1229 and it converges after 13 iterations.
Cite As
Farhad Sedaghati (2025). Newton's Method (https://www.mathworks.com/matlabcentral/fileexchange/52362-newton-s-method), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- MATLAB > Mathematics > Elementary Math > Polynomials >
Tags
Acknowledgements
Inspired: newtonraphson
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Newton's Method to find the roots of a polynomail/
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 |
Updated description
|