rootSolve(func, xLow, xUpp, tol)
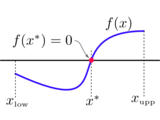
This function uses Ridder's Method to do non-linear root finding. This method works well for smooth scalar functions, and requires a bounded search space.
% XZERO = ROOTSOLVE(FUNC, XLOW, XUPP, TOL)
%
% FUNCTION: This function uses Ridder's Method to return a root, xZero,
% of func on the interval [xLow,xUpp]
%
% INPUTS:
% func = a function for a SISO function: y = f(x)
% xLow = the lower search bound
% xUpp = the upper search bound
% tol = return xZero if abs(func(xZero)) < tol
%
% OUTPUTS:
% xZero = the root of the function on the domain [xLow, xUpp]
%
% NOTES:
% 1) The function must be smooth
% 2) sign(f(xLow)) ~= sign(f(xUpp))
% 3) This function will return a root if one exists, and the function is
% not crazy. If there are multiple roots, it will return the first one
% that it finds.
Cite As
Matthew Kelly (2024). rootSolve(func, xLow, xUpp, tol) (https://www.mathworks.com/matlabcentral/fileexchange/54458-rootsolve-func-xlow-xupp-tol), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxTags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.21.0.0 | updated documentation |
||
| 1.2.0.0 | Added feature: the user can now specify the convergence tolerance. Fixed a small bug: the tolerance for checking roots on the boundary of the interval was set to 0, rather than the convergence tolerance. |
||
| 1.1.0.0 | Added photo. |
||
| 1.0.0.0 |