Random close packing (RCP) on arbitrary distribution of circle sizes
# Input / Output
function [NWP,NWR] = pack_v(f) ... outputs positions of circles (NWP) and corresponding radii (NWR) given an input vector (f) of radii size.
# Result Example
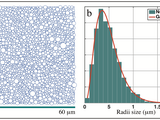
Packing result for N=3332 circles, Gamma distributed in size with shape factor 3.81, is shown in result_v1.png
# Motivation & Theory
Updated March 09 2016.
This algorithm produces random close packing or RCP on an input of N radii following any arbitrary distribution of size. The script was developed as part of my PhD project, which involves modelling white matter microstructure. White matter bundles in the human brain consist of axons (or hollow cylinders) running uni-directionally. A 2-dimensional cross section of such a cylindrical bundle can be represented by a packing of circles. In human anatomy, axon size follow a Gamma distribution. Conventional software for biophysical modeling (for example, UCL's Camino Diffusion MRI toolkit) generates packing densities up to 65%. However, axon density in white matter regions such as the corpus callosum can reach densities up to 85%, based on literature values.
This algorithm is developed with motivation from electromagnetic theory. Given N charged particles, the task cast is to produce the configuration of maximum potential energy by minimizing the sum of distances of the circles - the assumption being that such a configuration is equivalent to or at least close to that of maximum packing density.
This is performed iteratively. A pool of N circles is generated. Next, a circle is selected at random without replacement. The placement or position of the selected circle is determined such that its distance to the average center of the circles already placed is minimized. This process is iterated.
For small N (~50) algorithm takes ~2 minutes with 8GB of RAM. For large N (~3000), algorithm takes ~10 hours. To confirm the method's robustness on first pass, if the input is circles of uniform size, it converges to hexgonal close packing (HCP).
Cite As
Ti Xu (2024). Random close packing (RCP) on arbitrary distribution of circle sizes (https://github.com/BluesBlues213/random-close-packing), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
Versions that use the GitHub default branch cannot be downloaded
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 | results_v1.png Added notes on algorithm speed. |
|