Karhunen-Loeve Decomposition for Statistical Recognition and Detection
Karhunen-Loeve Decomposition for Face Recognition
You are now following this Submission
- You will see updates in your followed content feed
- You may receive emails, depending on your communication preferences
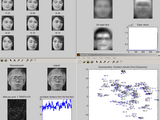
This MATLAB script implements Karhunen-Loeve decomposition which is classical algorithm for face recognition and detection. Script uses ATT faces database http://www.uk.research.att.com/facesataglance.html
which can be downloaded from
http://www.uk.research.att.com/facedatabase.html
Computing Eigenvalues and Eigenvectors of images set
Encoding Face Images with a Linear Combination Key (KL decomposition)
Decoding a Key into an Image (reconstruction)
Comparing images using key, searching for similar images.
Cite As
Alex Chirokov (2026). Karhunen-Loeve Decomposition for Statistical Recognition and Detection (https://www.mathworks.com/matlabcentral/fileexchange/6995-karhunen-loeve-decomposition-for-statistical-recognition-and-detection), MATLAB Central File Exchange. Retrieved .
Acknowledgements
Inspired: Karhunen-Loeve Transform Demonstration for Image Compressing
Categories
Find more on Dimensionality Reduction and Feature Extraction in Help Center and MATLAB Answers
General Information
- Version 1.0.0.0 (1.52 KB)
-
No License
MATLAB Release Compatibility
- Compatible with any release
Platform Compatibility
- Windows
- macOS
- Linux
| Version | Published | Release Notes | Action |
|---|---|---|---|
| 1.0.0.0 | Code was updated to find the most similar and the most different faces. Also distance map of face database is now computed and shown. |
