Sines and Splines - Variable Projection
Version 1.0.4 (318 KB) by
Johannes Handler
Separating periodic signals from their aperiodic background
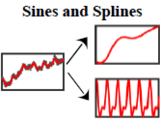
"Sines and Splines - Variable Projection" demonstrates the separation of a signal into its periodic and aperiodic portions, whereby the period of the periodic portion is unknown. Therfore the signal is modelled by a linear combination of nonlinear basis functions. The separation is done via the variable projection method, which splits the problem into a one-dimensional nonlinear optimization, combined with a linear least-squares computation.
This toolbox also provides a procedure for choosing an appropriate inital value for the nonlinear optimization.
An added benefit of this method is, that it also permits calculating the covanriances of the linear coefficients of the model, enabling the calculation of confidence and prediction intervals.
The periodic component is modelled by a set of harmonic basis functions. In this way any periodic shape can be modelled. The aperiodic component is modelled by a B-Spline.
The toolbox contains the following support functions:
harmonicBasis.m: creates a matrix with harmonic basis functions.
bSplineBasis.m: creates a matrix with the B-Spline basis functions.
bSplineBfn.m: support function for bSplineBasis.m
FFTReal.m: computes the positive half spectrum for a real input signal; this is needed for the selection of a suitable initial value of the nonlinear optimization
This code can also be considered as supplemental Material to the Paper:
"Modelling Periodic Measurement Data Having a Piecewise Polynomial Trend Using the Method of Variable Projection"
by: Johannes Handler, Dimitar Ninevski and Paul O'Leary
October 2023
https://arxiv.org/pdf/2109.07289.pdf
This paper presents a method for modelling periodic signals having an aperiodic trend using the method of variable projection. In particular, this paper focuses on using B-Splines to model the a-periodic portion. The MATLAB files presented here implement the numerical testing of the method with specific examples.
Additionally, the paper presents a thorough algebraic formulation of the method, as well as a comparison to using global polynomial approximation. It is proven that splines work better for modelling a more complicated aperiodic portion when compared to higher order polynomials. An added benefit of using the method of variable projection is the possibility to calculate the covariances of the linear coefficients of the model, which enable the calculation of confidence and prediction intervals.
@INPROCEEDINGS{Handler2023,
author={Handler, Johannes and Ninevski, Dimitar and O’Leary, Paul},
booktitle={IECON 2023- 49th Annual Conference of the IEEE Industrial Electronics Society},
title={Modelling Periodic Measurement Data Having a Piecewise Polynomial Trend Using the Method of Variable Projection},
year={2023},
pages={1-8},
doi={10.1109/IECON51785.2023.10312537}}
Further information about this topic can also be found in,
@inproceedings{OLeary2021,
author={O'Leary, Paul and Ninevski, Dimitar},
booktitle={2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC)},
title={Estimating Parameters of a Sine Wave by the Method of Variable Projection},
year={2021},
pages={1-6},
doi={10.1109/I2MTC50364.2021.9459842}}
@INPROCEEDINGS{Handler2021,
author={Handler, Johannes and Ninevski, Dimitar and O’Leary, Paul},
booktitle={2021 7th International Conference on Mechanical Engineering and Automation Science (ICMEAS)},
title={Decomposition of a Periodic Perturbed Signal with Unknown Perturbation Frequency by the Method of Variable Projection},
year={2021},
pages={44-49},
doi={10.1109/ICMEAS54189.2021.00019}}
Cite As
Handler, Johannes, et al. “Modelling Periodic Measurement Data Having a Piecewise Polynomial Trend Using the Method of Variable Projection.” IECON 2023- 49th Annual Conference of the IEEE Industrial Electronics Society, IEEE, 2023, doi:10.1109/iecon51785.2023.10312537.
MATLAB Release Compatibility
Created with
R2020b
Compatible with any release
Platform Compatibility
Windows macOS LinuxTags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.