polyval
Polynomial evaluation
Description
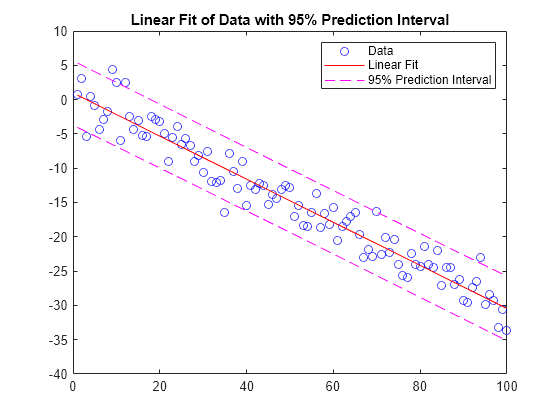
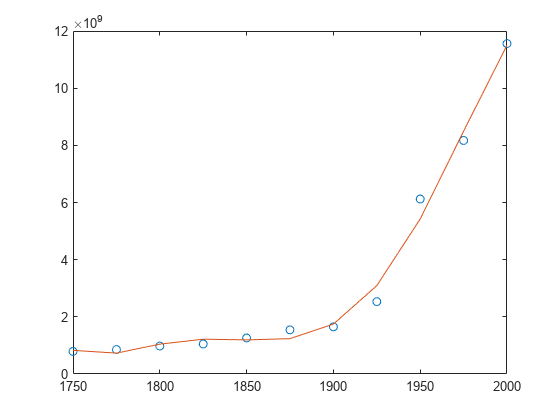
y = polyval(p,x)p at each point in x.
The argument p is a vector of length n+1 whose
elements are the coefficients (in descending powers) of an
nth-degree polynomial:
The polynomial coefficients in p can be calculated for
different purposes by functions like polyint, polyder, and polyfit, but you can specify any
vector for the coefficients.
To evaluate a polynomial in a matrix sense, use polyvalm instead.
y = polyval(p,x,[],mu)[
use the optional output y,delta]
= polyval(p,x,S,mu)mu produced by polyfit to center and scale the
data. mu(1) is mean(x), and
mu(2) is std(x). Using these values,
polyval centers x at zero and scales it to
have unit standard deviation,
This centering and scaling transformation improves the numerical properties of the polynomial.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced before R2006a