butter
Butterworth filter design
Syntax
Description
[
designs a lowpass, highpass, bandpass, or bandstop digital Butterworth filter,
depending on the value of b,a] = butter(n,Wn,ftype)ftype and the number of elements
of Wn. The resulting bandpass and bandstop filter designs
are of order 2n.
Note
You might encounter numerical instabilities when designing IIR filters with transfer functions for orders as low as 4. See Transfer Functions and CTF for more information about numerical issues that affect forming the transfer function.
[
designs a digital Butterworth filter and returns its zeros, poles, and gain.
This syntax can include any of the input arguments in previous syntaxes.z,p,k] = butter(___)
[___] = butter(___,"s") designs
an analog Butterworth filter using any of the input or output arguments in
previous syntaxes.
[
designs a lowpass digital Butterworth filter using second-order Cascaded Transfer Functions
(CTF). The function returns matrices that list the denominator and numerator
polynomial coefficients of the filter transfer function, represented as a
cascade of filter sections. This approach generates IIR filters with improved
numerical stability compared to with single-section transfer functions. (since R2024b)B,A] = butter(n,Wn,"ctf")
[___] = butter(
designs a lowpass, highpass, bandpass, or bandstop digital Butterworth filter,
and returns the filter representation using the CTF format. The resulting design
sections are of order 2 (lowpass and highpass filters) or 4 (bandpass and
bandstop filters). (since R2024b)n,Wn,ftype,"ctf")
[___,
also returns the overall gain of the system. You must specify
gS] = butter(___)"ctf" to return gS. (since R2024b)
Examples
Input Arguments
Output Arguments
More About
Algorithms
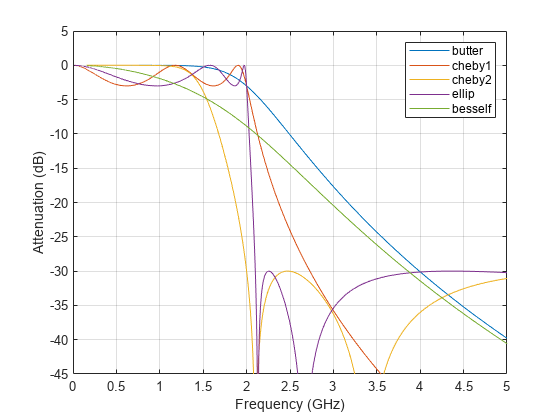
Butterworth filters have a magnitude response that is maximally flat in the passband and monotonic overall. This smoothness comes at the price of decreased rolloff steepness. Elliptic and Chebyshev filters generally provide steeper rolloff for a given filter order.
butter uses a five-step algorithm:
It finds the lowpass analog prototype poles, zeros, and gain using the function
buttap.It converts the poles, zeros, and gain into state-space form.
If required, it uses a state-space transformation to convert the lowpass filter into a bandpass, highpass, or bandstop filter with the desired frequency constraints.
For digital filter design, it uses
bilinearto convert the analog filter into a digital filter through a bilinear transformation with frequency prewarping. Careful frequency adjustment enables the analog filters and the digital filters to have the same frequency response magnitude atWnor atw1andw2.It converts the state-space filter back to its transfer function or zero-pole-gain form, as required.
References
[1] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.