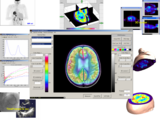
mia - medical image analysis
This Matlab GUI enables you to do analysis on medical images. A collection of tools are provided to perform slice or volume based analysis. On the other hand the program can be considered as a wrapper of useful previously developed and own matlab tools for medical image processing. The following new features are included in the latest version:
For more information about the all included options of mia find the "miahistory.doc" file at
http://petunia.atomki.hu/~balkay/mia/miahistory.doc
Installing, running: unzip the downloaded file, you will have a mia directory containing the whole utility. Add the mia directory (and ALL subfolders) to your matlab path. Run the mia function.
Before installation delete the previous version of MIA if exists.
Cite As
Laszlo Balkay (2024). Mia 2.5 (https://www.mathworks.com/matlabcentral/fileexchange/4706-mia-2-5), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Test and Measurement > Instrument Control Toolbox > Instrument Control Toolbox Supported Hardware >
- Industries > Medical Devices > DICOM Format >
Tags
Acknowledgements
Inspired by: Sliceomatic
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.