Atmospheric Carbon Dioxide Modeling and the Curve Fitting Toolbox
By Mary Ann Branch, MathWorks and Russ Minkwitz, MathWorks
A common measurement for studying the effect of burning fossil fuels on weather patterns is the level of carbon dioxide (CO2) concentration in the atmosphere. Some scientists believe the upward trend in CO2 levels could cause atmospheric temperatures to rise, polar ice caps to melt, and climates of different regions of the earth to change radically.
Since this data has cyclical phenomena, as well as an upward growth trend, nonlinear fitting techniques are appropriate, but can require added effort when compared to fitting a linear model. However, with the right tools and knowledge of your data, you can quickly determine the coefficients of a nonlinear model.
This article describes how to fit a nonlinear model to available CO2 data using the newly released Curve Fitting Toolbox.
Modeling the Data
In this example, we use CO2 data, in parts per million, collected by the U.S. National Oceanic and Atmospheric Administration (NOAA) from 1979 to 1996 at the Mauna Loa Observatory in Hawaii2. The captured data is shown in the following illustration.

Cyclical phenomena in nature can be modeled by a sinusoid and its higher harmonics, that is,


where t (time) is in years, α is believed to be approximately 0.0444/year, and the other parameters are unknown (including the number of sinusoids needed)2.
To build the model, we go to the Curve Fitting Toolbox's Fitting GUI and create a custom equation with one sinusoid term.

Because the time values are large, we can select the option to center and scale the time variable (remove the mean and divide by the standard deviation) to improve the conditioning of the numerical calculations.
Refining the Model
We can improve upon this model in several ways. First, we can determine the coefficients of the exponential term separately. We use the toolbox's built-in exponential model which automatically calculates optimal start points from the data,
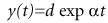
Now we can plot the residuals that still show a cyclical sinusoid pattern, so another sinusoid term is warranted.
Extending the Analysis
When we have found a satisfactory model, we can send our fits to the MATLAB workspace for further analysis. We have several other observatory sites to examine (e.g., Samoa, the South Pole, and Barrow) and so can generate an M-file function that can recreate our fits. Then we can call the function in a loop to automatically fit other data sets to see how the resulting models compare across observatory sites.
This example touches on a few of the features that will help you fit models to data. Whether the models are linear or nonlinear, the Curve Fitting Toolbox enables you to quickly fit standard models from its library or custom models you create.
Published 2002 - 91034v00
References
-
GLOBALVIEW-CO2, "Cooperative Atmospheric Data Integration Project - Carbon Dioxide" (2001). [Available to the public at ftp.cmdl.noaa.gov, Path: ccg/co2/GLOBALVIEW]
-
Kahner, D., Moler, C., Nash, S., Numerical Methods and Software, Prentice Hall (1989)




