Building Accurate, Realistic Simulink Models
By Seth Popinchalk, MathWorks
An accurate system model is one that performs as expected and produces the desired results. To achieve this level of accuracy you must have a clear modeling goal. For example, will the model be used strictly for simulation, or for generating embedded C code?
This article describes five modeling techniques that can help ensure accuracy:
We discuss the choices and assumptions made at the early modeling stages and examine techniques for asserting under what conditions (parameter ranges) the model will be valid. Finally, we apply these techniques to the challenging problem of handling mode changes in an anti-lock breaking system.
Select the Right Modeling Approach
In Simulink you can model using a system-level (top-down) or detail-by-detail (bottom-up) approach. The starting point determines how the model will be organized. In a system-level model, the interfaces between components are laid out and progressively elaborated. In the detail-by-detail approach the model grows organically as you add complexity over time.
With either approach you can use domain-specific modeling tools, such as SimMechanics, SimHydraulics and Simscape Electrical, to implement the model components. These tools maintain the design specification in a familiar schematic format and automatically derive equations based on first principles.
Components not easily modeled with domain-specific tools can be built from a first-principles physical understanding of the system. You implement the equations that govern the system with blocks that perform basic math operations—for example, you might begin with a free body diagram to discover the forces acting on an object.
Component-level models can also be implemented using pre-existing data from the physical system. You use this approach when test data is available or to simplify complicated dynamics equations.
Know your System, Understand its Dynamics
To achieve accuracy in a model, you must configure the simulation parameters to give good results—for example, by selecting the proper tolerance settings of a variable step solver to optimize the trade-off between model performance and state calculation accuracy. To configure the parameters accurately you must understand the nature and dynamics of the physical system.
You may not know the dynamics of a complicated system with hundreds or thousands of components until you have connected all the components and simulated the entire model. In this case, you must test each component as you model it. You then build a test harness for each component and maintain its interface as the larger model evolves.
Knowing your system involves understanding its dynamics so that the simulation parameters can be configured to accurately capture the results. You can determine the system’s frequency response by creating a linearized representation of the model using Simulink and Simulink Control Design. ( For details, see the Simulink Control Design documentation.) A linear representation limits your understanding to behavior over a defined range of inputs and state values. Identifying the step sizes required to capture the full system dynamics, requires a variable step solver.
Monitor for Unacceptable Results
Simulink includes a library of blocks for monitoring simulation results. The Model Verification blocks let you monitor a signal for its value, set static or dynamic bounds, and throw assertions when these bounds are violated. For example, in modeling the dynamics of an aircraft braking system that will make the aircraft decelerate after touchdown, you might be limited by the maximum allowable deceleration. You can build this limitation into a subsystem with the Check Static Range block (Figures 1 and 2).
Verify Simulation Results
Ensuring that a model generates values in an expected range does not guarantee good results. You must also consider what type of signal you are monitoring. For example, integrators and transfer functions, like low-pass filters, often smooth their outputs. This filtering effect can hide non-realistic dynamics in the system. Consider, for example, acceleration, speed, and position. By observing position or speed but not the acceleration signal, it is easy to overlook high-frequency changes in acceleration. A noisy acceleration can still produce a smooth speed signal (Figure 3).
Understand Modeling Assumptions
We have seen how the choice of implementation affects model accuracy and reviewed some best practices for building in assertions and verifying results. To ensure a model’s accuracy it is also important to record any assumptions with the model, such as the maximum allowable input current for an actuator. The model then becomes an executable specification that is the primary source of information about the system’s behavior.
Example: Modeling an Anti-Lock Braking System
The anti-lock braking system model (Figure 4) contains continuous-time dynamics modeled from first principles, a look-up table to relate relative slip to the coefficient of friction, and a model reference component to encapsulate the wheel speed calculation. Because the model is simple, it was implemented using a bottom-up approach, starting not from a specification and system design, but from equations.
In this system, the wheel’s surface speed (ωw) becomes less than the velocity of the vehicle (ωv) as a brake is applied to a wheel. The relative slip (1- ωw / ωv) changes the amount of friction between the wheel and the road, which in turn determines the braking force. Our system aims to apply a brake pressure that will keep the maximum brake force and avoid lock-up.
This simple model can easily be turned into a component in a larger vehicle model (Figure 6).
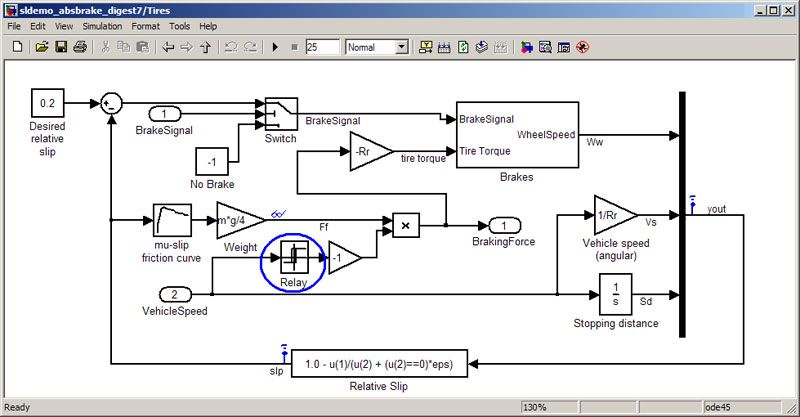
The tire subsystem (Figure 7) is functionally the same as the original model, but now it accepts a brake signal that toggles between applying the brakes (BrakeSignal > 0) and no brakes (BrakeSignal < 0).
This tire component could now become part of a larger vehicle simulation. We can verify that the component behaves as expected by using a signal builder block to schedule a brake test in which the brakes are applied for 2 seconds, disengaged for 7 seconds, and then reapplied until the vehicle stops.
The results are as we might expect: The original vehicle model stops the simulation as soon as the vehicle stops. If we remove the Stop Block from the model, we learn that one of the assumptions made in the model was that the vehicle speed will never be zero.
Now the simulation runs, but it seems to stall. When it eventually completes, it shows an error report indicating that consecutive zero crossings are slowing down simulation.
The variable step solver keeps detecting a zero crossing because the brake force signal to the vehicle is negative but the state has reached its zero limit. The solver throws this error before we can determine what the problem is. If we had used a fixed-step instead of a variable-step solver, the simulation would have had to continue beyond this point.
We change to the fixed-step ODE3 solver. The simulation now shows a strange condition where, after being at rest for a short period, the vehicle suddenly jumps from 0 to high speed in zero time (Figure 10). Something is wrong with the model.
The problem is that the brakes don’t handle the condition where the vehicle is stationary. The torque on the wheels remains after the parts are at rest, which is not correct. We avoided this error in the original model by limiting the simulation to the region where it was valid. To work around it in this model we must either correct the model or build in those assumptions.
An assertion block lets you issue a warning whenever the simulation hits a condition for which this model is not valid (Figure 11).
When the vehicle speed is less than or equal to zero, the model is no longer valid. Again, we could stop the model when the vehicle speed is zero. We don’t need to do this, however, because we included additional information to assert the reason why, and provided a callback to report the assertion (Figure 12).
To remedy the problem we must add the following conditions:
- The model accounts for stick and slip friction on the brakes.
- The tires apply a braking force on the vehicle only if the vehicle is moving.
- Brake force always functions in opposition to vehicle velocity.
Building a Model that Changes Mode
We will now add elements to the model to allow the vehicle to come to rest. The desired behavior can be translated into the following equations for torque and force:
\[\begin{align}T_{\text{net}} &= \begin{cases} T_{\text{tire}} - T_{\text{brake}} & \omega_{\text{wheel}} \neq 0 \\ T_{\text{tire}} - \min(T_{\text{brake}},T_{\text{tire}}) & \omega_{\text{wheel}} = 0 \end{cases} \\ F_{\text{brake}} &= \begin{cases} -\text{sign}(V_{\text{vehicle}})|F_{\text{brake}}| & V_{\text{vehicle}} \neq 0 \\ 0 & V_{\text{vehicle}} = 0\end{cases}\end{align}\]
To implement these equations we simply add switching logic to the Tire subsystem via the Signum Block (Figure 13).
The output of the Signnum block will be 1 for a positive input, -1 for negative input, and 0 for zero input. Now the brake force will always resist vehicle speed, and it should enable us to remove vehicle speed saturation. We add a switch to the Brakes subsystem to prevent the break torque from turning the wheel in the opposite direction after it stops (Figure 14).
The Switch block holds the switching condition where we pass through input 1 when input 2 is not equal to zero. Monitoring u2 ~= 0 should enable us to remove the lower saturation limit on the wheel speed. Simulating the model now using ODE45 results in a negative wheel speed (Figure 15).
If we add the saturation of the wheel speed back into the model, the simulation looks correct, but we get consecutive zero crossing errors, and the simulation stops (Figure 16).
These errors come from the newly added Signum block. Both the equations that we implemented rely on an exact zero value to achieve the stable condition. If the solver doesn’t set these control signals exactly to zero, the results are as we saw.
Let’s look at a signal whose output is directly computed by the Signum block: the brake force (Figure 17).
Since the equations require brake force to oppose vehicle velocity or be zero, the spike at the end of the simulation signals a potential problem. Zooming in on this area we see that the switching of the Signum block has resulted in model chattering. The numbers sometimes reveal this behavior more clearly.
>> Fbrake.Data(end-5:end)
ans =
281.5750
-281.5750
281.5750
-281.5750
281.5750
-281.5750
The step size over this period is extremely small because the variable step solver is detecting and searching for the exact zero crossing. Here, the power of the solver and the extremely fragile discontinuity that we have introduced result in the simulation effectively stopping. The solver was taking its minimum step size in an effort to ensure accuracy.
>> diff(Fbrake.Time(end-6:end))
ans =
1.0e-012 *
0.3340
0.3340
0.3340
0.3340
0.3340
0.3340
Without the repeated zero crossing diagnostic, the model would have continued to take steps at this rate until the simulation ended. If we were unaware of this condition, we might assume that Simulink had frozen or that our system was crashing. In fact, full computing resources were being devoted to completing the simulation at this minute step size.
Hysteresis can resolve this type of mode switching. Hysteresis is common in physical systems where the reaction of the system depends on the past history of the system. For example, thermostats are designed with hysteresis to avoid rapid switching between on and off. The switch may turn on when temperature is a degree below the set point and then turn off when the temperature is two degrees above it.
Using the Relay block from the Discontinuities library rather than the Signum block lets us handle this condition with some tolerance (Figure 18).
The model still assumes positive initial vehicle velocity and is not yet completely generalized for both directions of motion. We can also apply hysterisis to the tire velocity output (Figure 19).
Summary of Best Practices
A thorough understanding of the system dynamics makes it much easier to set up the initial configuration of the model and lets you build in monitoring of incorrect results. The model must incorporate all design assumptions. One effective way to do this is to use assertion blocks to monitor for invalid inputs to the model. Heuristics can be applied to correct behavior within models that encounter chattering conditions due to the solver-system interactions. Ultimately, modeling for accuracy requires testing of individual components and a clear understanding of the system being modeled.
The models referenced in this article can be downloaded from MATLAB Central.
Published 2006