Cascade Digital PID Control Design for Power Electronic Converters
By Zhao Wang, Siddharth Jawahar, Antonino Riccobono, and Arkadiy Turevskiy, MathWorks
This article is the third in a three-part series. Part 1, Estimating the Frequency Response of a Power Electronics Model, introduces a six-step workflow for estimating the frequency response of an open-loop boost converter. Part 2, Estimating the Frequency Response of a Power Electronic Model: Sinestream vs. Pseudo-Random Binary Sequence (PRBS), compares frequency response estimation (FRE) for an open-loop buck converter with sinestream and with PRBS, focusing on estimation time, number of estimated frequency points, and estimation accuracy. Please refer to the Multiloop Control Design for Buck Converter example.
Switch-mode power electronics converters modeled with Simscape Electrical™ components often use a cascade PID control architecture, which offers fast output voltage response with controllable current dynamics. Since switch-mode converters are discontinuous and cannot be linearized analytically, before tuning the PID controller gains in the cascade configuration you can compute a linear time-invariant estimation of the plant model using Simulink Control Design™ tools for frequency response estimation (FRE).
In FRE, the transfer function of the plant model is estimated at discrete frequency points, starting from the injection of a signal of controllable amplitude and frequency to the model operating in steady state. The estimated plant transfer function can be used for tuning the controller gains to meet closed-loop performance requirements.
Using a buck converter as an example, this article describes a seven-step workflow for tuning the gains of a discrete PID controller in a cascade control configuration. This configuration typically consists of an inner current-loop and an outer voltage-loop. The workflow is completed first for the inner loop and then for the outer loop. The inner loop is designed first to ensure that the outer loop, with its lower bandwidth, has a minimal effect on the inner loop stability margins.
Buck Converter Model
A buck converter is a power electronics topology that can supply a load with a DC voltage that is lower than the DC supply voltage. It is widely used in many applications with different power ratings, including consumer electronics products, electric automobiles, more-electric ships and aircraft, renewables, and LED drivers.
Figure 1 shows a switch-mode buck converter modeled with Simscape Electrical components to provide a voltage regulation from 48 V to 12 V. The switching frequency of the buck converter is 100 kHz. The PWM sample rate is 100 times faster than the switching frequency to provide a 1% duty cycle resolution. The cascaded control architecture is designed so that the inner loop regulates the inductor current and the outer loop regulates the output voltage. The output of the outer voltage loop provides the current reference signal to the inner current loop, which, in turn, provides the duty cycle signal to the PWM Generator block. To mimic a digital controller, sampling is included in the controller model. Since the inner and outer loops control similar dynamics, the sample time for both loops is set at 1e-5 seconds to match the switching period.
The controller architecture includes manual switches to make the converter operate in one of three configurations: open-loop (PWM Generator block with a constant duty cycle); inner current-loop; and outer voltage loop.
When the converter is simulated in the open-loop configuration, the results reveal a poor regulation of inductor current and output voltage in the presence of load and input voltage disturbances, respectively (Figure 2). Closed-loop control with properly tuned PID controllers is required to improve current and voltage regulation.
Control Design Workflow: Inner-Loop Current Controller
Using FRE tools in Simulink Control Design, the steps are as follows:
- Set the required loop configuration through the Manual Switch blocks.
- Find a snapshot-based operating point and initialize the model.
- Specify which portion of the model requires FRE.
- Create a perturbation signal for the FRE experiment.
- Compute the nonparametric plant model.
- Tune the controller gains using the nonparametric plant model.
- Verify the tuned controller's performance.
1. Set the open-loop configuration
Make sure that the Manual Switch block (“Switch1” in Figure 1) is positioned so that it connects the PWM Generator block input to the Constant block named “Duty Cycle.”
2. Find a snapshot-based operating point and initialize the model
To capture system dynamics accurately, FRE must be performed at steady state. From the Operating Point dropdown menu in the Estimation tab of the Model Linearizer app, compute a simulation snapshot at 0.007 seconds (Figure 3, red). The simulation results indicate that the model reaches steady state at that simulation time (Figure 2). You can use the computed simulation snapshot to initialize the model (Figure 3).
3. Specify which portion of the model requires FRE
From the Linearization Manager toolstrip, assign “Input Perturbation” to the output signal of the Constant block named “Duty Cycle” and “Output Measurement” to the output of the Rate Transition block named “Current ADC” (Figure 4).
4. Create a perturbation signal for the FRE experiment
From the Input Signal dropdown menu in the Estimation tab of the Model Linearizer app, select PRBS Pesudorandom Binary Sequence (Figure 5, left). To balance estimation speed and accuracy, the PRBS perturbation signal is configured with the parameters shown in Figure 5. An object in_prbs1 is created in the app workspace once you click “OK.”
5. Compute the nonparametric plant model
Before starting the FRE, find the time-varying sources. These must be held constant during the experiment (Figure 6, left). Start the experiment by clicking “Bode” (Figure 6, middle). During simulation, the PRBS signal is injected into the duty cycle signal and the response is measured at the sampled inductor current.
At the end of the experiment, a raw nonparametric model estsys1 is created. This model is a description of the system at discrete frequency points. Use the “Result Thinning” button in the Plots and Results tab to thin the estimation over 30 frequencies from 700 rad/s to 3e5 rad/s (Figure 6, right). After thinning, the object estsys1_thinned is created. The thinned result is much smoother than the raw estimation over the specified frequency range. Move the thinned object from the app workspace to the MATLAB® workspace so that you can use it for controller tuning.
Figure 6. Finding the time varying sources (left), raw nonparametric estimation (middle), and thinned nonparametric estimation (right) needed for tuning the inner-current loop.
6. Tune the controller gains using the non-parametric model
Set the current-loop configuration by using the Manual Switch blocks labeled “Switch1” and “Switch2” in Figure 1, and then complete these steps:
- Open the block dialog for the Discrete PID Controller block in the inner loop and click “Tune” to launch the PID Tuner app.
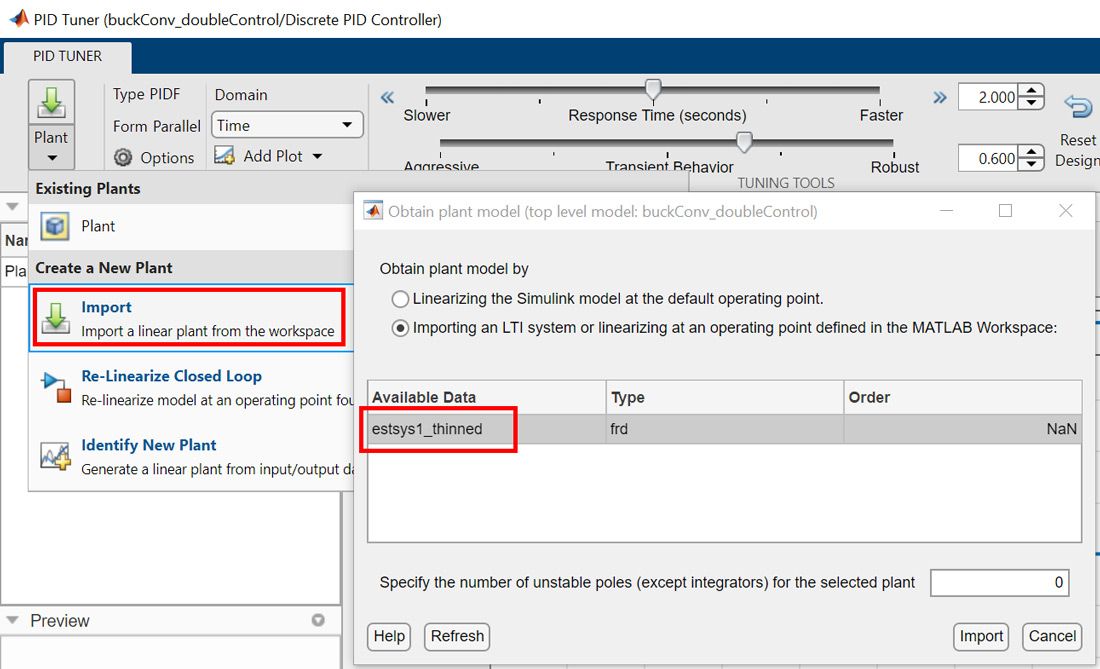
- Ignoring the linearization failure message, import the object
estsys1_thinned(Figure 7, left). - Configure the app to perform the tuning in the frequency domain (Figure 7, right).
- Select a bandwidth that is about 10 times smaller than the Nyquist frequency, or half the switching frequency (for example, 3e4 rad/s).
- Select 60 degrees as the phase margin (for well-damped response).
- Click “Update Block” to apply the tuned gain values to the Discrete PID Controller block in the inner loop.
Figure 7. Importing the thinned nonparametric estimation (left) and tuning the PID control gains (right) of the inner current loop.
7. Verify the tuned controller performance
Before tuning the outer loop, it is good practice to verify the performance of the tuned inner loop in both time and frequency domains. To do this, make sure that the first Manual Switch block (“Switch1” in Figure 1) connects the PWM Generator block's input to the PID Controller block in the inner loop while maintaining the position of the second Manual Switch block (“Switch2” in Figure 1).
Simulation with this current-loop configuration reveals that the inductor current is now regulated but the output voltage is not (Figure 8).
Next, perform an FRE-based verification by estimating the inner control open-loop transfer function. The goal is to achieve the bandwidth and phase margin targets. From the Linearization Manager toolstrip, assign “Loop Transfer” to the output signal of the Discrete PID Controller block in the inner loop and remove the existing linearization I/Os (Figure 9, left). Re-initialize the model using a new simulation snapshot operating point. You can then start another experiment using the same PRBS perturbation signal.
After thinning and correcting for the 180° phase shift caused by the negative sign in the feedback loop, you can verify that the result shown in Figure 9 is identical to the tuning result in the PID Tuner app shown in Figure 7.
Figure 9. Left: Loop transfer at the output of the inner-loop Discrete PID Controller block added from the Linearization Manager toolstrip. Right: Open-loop Bode plot verifying the stability margins of the inner current-loop.
Control Design Workflow: Outer-Loop Voltage Controller
Having tuned the inner current-loop, you can tune the controller gains in the outer voltage-loop, using the same seven-step procedure but with the inner loop closed.
1. Set the current-loop configuration
Make sure that the position of the Manual Switch block (“Switch 2” in Figure 1) connects the Constant block "Iref" to the Discrete PID Controller block in the inner loop.
2. Find a snapshot-based operating point and initialize the model
Compute a simulation snapshot operating point at 0.007 seconds to initialize the buck converter model with the inner current loop.
3. Specify which portion of the model requires FRE
From the Linearization Manager toolstrip, assign “Input Perturbation” to the output signal of the Constant block named “Iref” and “Output Measurement” to the output of the Rate Transition block named “Voltage ADC” (Figure 10).
4. Create a perturbation signal for the FRE experiment
You can use the same PRBS input signal that you defined for the inner-loop current controller. All the parameters are identical except for amplitude, which is increased from 0.05 to 1 to improve the signal-to-noise ratio.
5. Compute the nonparametric plant model
Click “Bode” to start the estimation. During the estimation process, the PRBS signal is injected into the current reference signal and the response is measured at the sampled output voltage. Thin the raw nonparametric estimation over 30 frequencies from 700 rad/s to 2e5 rad/s and move the thinned object to the MATLAB workspace. Figure 11 shows the raw and thinned nonparametric results.
Figure 11. Raw nonparametric estimation (left) and thinned nonparametric estimation (right) needed for tuning the outer voltage-loop.
6. Tune the controller gains using the nonparametric plant model
Enable the voltage-loop configuration by changing the position of the Manual Switch block labeled “Switch2” in Figure 1 and then do the following:
- Launch the PID Tuner app from the Discrete PID Controller block in the outer loop.
- Import the thinned nonparametric object that you estimated in the previous step.
- Tune the controller gains by setting the bandwidth to 3e3 rad/s (typically, the outer loop is tuned to be 10 times slower than the inner loop) and the phase margin to 60 degrees (Figure 12).
- Click “Update Block.”
7. Verify the tuned controller performance
Run the simulation to verify that the output voltage is well regulated at 12 V (Figure 13).
For the frequency-domain verification, conduct another FRE experiment by setting the output of the outer-loop Discrete PID Controller block as “Loop Transfer” to estimate the outer control open-loop transfer function (remember to remove all linearization I/Os previously set). Re-initialize the model from a new simulation snapshot taken at 0.007 seconds. Start the estimation by reusing the PRBS signal defined in step 4. After result thinning and correcting for the 180° phase shift caused by the negative sign in the feedback loop, you can verify that the result shown in Figure 14 is identical to the tuning result shown in the PID Tuner app (Figure 12).
Figure 14. Left: Loop transfer at the output of the outer-loop Discrete PID Controller block added from the Linearization Manager toolstrip. Right: Open-loop Bode plot verifying the stability margins of the outer voltage loop.
Summary and Next Steps
This article described an FRE-based control design workflow for tuning the controller gains of a switch-mode buck converter with an inner current control loop and an outer voltage control loop. The same workflow can be applied to switch-mode power electronics topologies with single-stage control architectures.
Now that both inner and outer loop PID controllers have been tuned and verified in the simulation environment, the design is ready for implementation on a microcontroller or FPGA.
Published 2022