Antenna Toolbox Coordinate System
Antenna Toolbox™ uses two types of coordinate system: rectangular coordinate system and spherical coordinate system.
Antenna Toolbox uses the rectangular coordinate system to visualize antenna or array geometry. The toolbox uses the spherical coordinate system to visualize antenna radiation patterns.
Rectangular Coordinate System
Visualize the geometry of a default monopoleTopHat antenna from
the antenna library.
m = monopoleTopHat; show(m);

The toolbox displays the top-hat monopole antenna in the rectangular or Cartesian coordinate system.
The rectangular coordinate system also called
Cartesian coordinate system specifies a position in space
as an ordered 3-tuple of real numbers, (x,y,z), with respect to
the origin (0,0,0).

You can view the 3-tuple as a point in space, or equivalently as a vector in three-dimensional Euclidean space. When viewed as a vector in space, the coordinate axes are basis vectors and the vector gives the direction to a point in space from the origin. Every vector in space is uniquely determined by a linear combination of the basis vectors. The most common set of basis vectors for three-dimensional Euclidean space are the standard unit basis vectors:
.
Orthogonal Basis and Euclidean Norm
Any three linearly independent vectors define a basis for three-dimensional space. However, the Antenna Toolbox assumes that the basis vectors you use are orthogonal.
The standard distance measure in space is the l2 norm, or Euclidean norm. The Euclidean norm of a vector [x y z] is defined by:
The Euclidean norm gives the length of the vector measured from the origin as the hypotenuse of a right triangle. The distance between two vectors [x0 y0 z0] and [x1 y1 z1] is:
Spherical Coordinate System
Visualize the radiation pattern of the default monopoleTopHat
antenna.
m = monopoleTopHat; pattern(m,75e6);
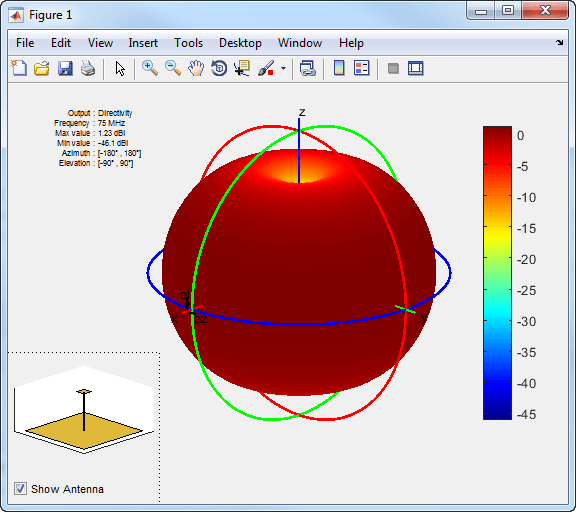
The toolbox displays the radiation pattern of the top-hat monopole using spherical coordinate system represented by azimuth and elevation angles.
The spherical coordinate system defines a vector or point in space with a distance R and two angles. You can represent the angles in this coordinate system:
Azimuth and elevation angles
Phi (Φ) and theta (θ) angles
u and v coordinates
Azimuth and Elevation Angles
The azimuth angle is the angle from the positive x-axis to the vector's orthogonal projection onto the xy plane, moving in the direction towards the y-axis. The azimuth angle is in the range –180 and 180 degrees.
The elevation angle is the angle from the vector's orthogonal projection on the xy plane toward the positive z-axis, to the vector. The elevation angle is in the –90 and 90 degrees.

Phi (Φ) and Theta (θ) Angles
The φ angle is the angle from the positive x-axis to the vector's orthogonal projection onto the xy plane, moving in the direction towards the y-axis. The azimuth angle is between –180 and 180 degrees.
The θ angle is the angle from the positive z-axis to the vector itself. The θ angle is in the range 0 degrees and 180 degrees.
These angles are an alternative to using azimuth and elevation angles to express the location of point in a unit sphere.

u and v Coordinates
You can define u and v in terms of φ and θ:
In terms of azimuth and elevation angles, the u and v coordinates are:
The values of u and v satisfy the inequalities:
The φ and θ angles in terms of u and v are:
The azimuth and elevation angles in terms of u and v are:
Conversion Between Rectangular and Spherical Coordinates
Convert rectangular coordinates to spherical coordinates (az, el, R) using:
Convert spherical coordinates (az, el, R) to rectangular coordinates using:
where:
R is the distance from the antenna
el and az are the azimuth and elevation angles
References
[1] Balanis, C.A. Antenna Theory: Analysis and Design. 3rd Ed. New York: Wiley, 2005.