Find Delay
Find delay between two signals
Libraries:
Communications Toolbox /
Utility Blocks
Description
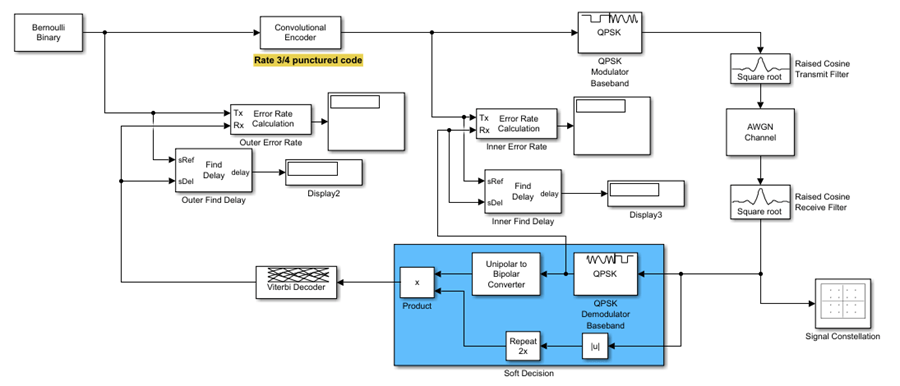
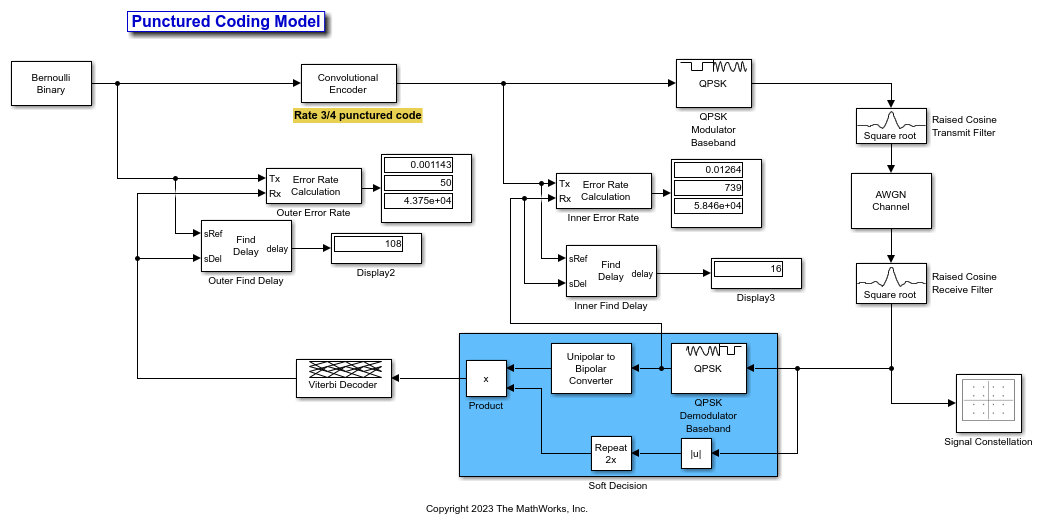
The Find Delay block finds the delay between a signal and a delayed, and possibly distorted, version of itself. This is useful when you want to compare a transmitted and received signal to find the bit error rate, but do not know the delay in the received signal. This block accepts a column vector or matrix input signal. For a matrix input, the block outputs a row vector, and finds the delay in each channel of the matrix independently. For more information about signal delays, see Delays in Communication Systems.
This icon shows the block with the optional chg port. ![]()
Examples
Ports
Input
Output
Parameters
Block Characteristics
More About
Tips
Set the Correlation window length (samples) parameter value sufficiently large so that the computed delay eventually stabilizes at a constant value. When this occurs, the signal from the optional chg output port stabilizes at the constant value of zero.
If the computed delay is not constant, you should increase correlation window length value.
If the increased value of correlation window length exceeds the duration of the simulation, then you should also increase the duration of the simulation accordingly.
If you can roughly estimate the delay, then the correlation window length will produce a stable delay estimate at four times that value.
If the cross-correlation between the two signals is broad, then the Correlation window length (samples) parameter value should be much larger than the expected delay, or else the algorithm might stabilize at an incorrect value. For example, a CPM signal has a broad autocorrelation, so it has a broad cross-correlation with a delayed version of itself. In this case, the Correlation window length (samples) value should be much larger than the expected delay.
If the block calculates a delay that is greater than 75 percent of the Correlation window length (samples) parameter value, the sRef signal is probably delayed relative to the sDel signal. In this case, you should switch the signal lines leading into the two input ports.
To configure the block stop updating the delay after it computes the same delay value for a specified number of samples, select Disable recurring updates, and enter a positive integer in the Number of constant delay outputs to disable updates field. For example, if you set Number of constant delay outputs to disable updates to
20, the block will stop recalculating and updating the delay after it calculates the same value20times in succession. Disabling recurring updates causes the simulation to run faster after the target number of constant delays occurs.
Algorithms
The Find Delay block finds the delay by calculating the cross-correlations of the first signal with time-shifted versions of the second signal, and then finding the index at which the cross-correlation is maximized.
Extended Capabilities
Version History
Introduced before R2006a