rlocus
Root locus plot of dynamic system
Description
rlocus( calculates and plots the root
locus of the SISO model sys)sys. The root locus returns the closed-loop
pole trajectories as a function of the feedback gain k (assuming
negative feedback). Root loci are used to study the effects of varying feedback gains on
closed-loop pole locations. In turn, these locations provide indirect information on the
time and frequency responses.
You can use rlocus to plot the root locus diagram of any of the
following negative feedback loops by setting sys
as shown below:
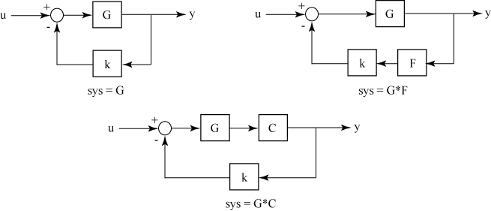
For instance, if sys is a transfer function represented by
the closed-loop poles are the roots of
The root locus plot depicts the trajectories of closed-loop poles when the feedback
gain k varies from 0 to infinity. rlocus
adaptively selects a set of positive gains k to produce a smooth
plot. The poles on the root locus plot are denoted by x and the zeros
are denoted by o.
rlocus(sys1,sys2,...) plots the root loci of multiple LTI models
sys1, sys2,... on a single plot. You can specify a color, line style,
and marker for each model. For even more plot customization options, see rlocusplot.
Examples
Input Arguments
Output Arguments
Tips
For an interactive approach to root locus plotting, see Control System Designer.
Version History
Introduced before R2006a
See Also
rlocusplot | tf | pole | zero | ss | zpk | Control
System Designer



